环形链表II

逻辑

快慢指针可以找到环形链表的原因

快慢指针是一种常用的解决链表问题的方法，特别是对于环形链表的问题。这种方法的基本思想是使用两个指针，一个快指针和一个慢指针，同时从链表的头部开始遍历。快指针每次移动两个节点，而慢指针每次移动一个节点。

如果链表中存在环，那么快指针和慢指针最终会在环中的某个位置相遇。这是因为快指针移动的速度是慢指针的两倍，所以即使快指针进入环后，慢指针还没有进入环，快指针也会在环中继续移动，最终追上慢指针。

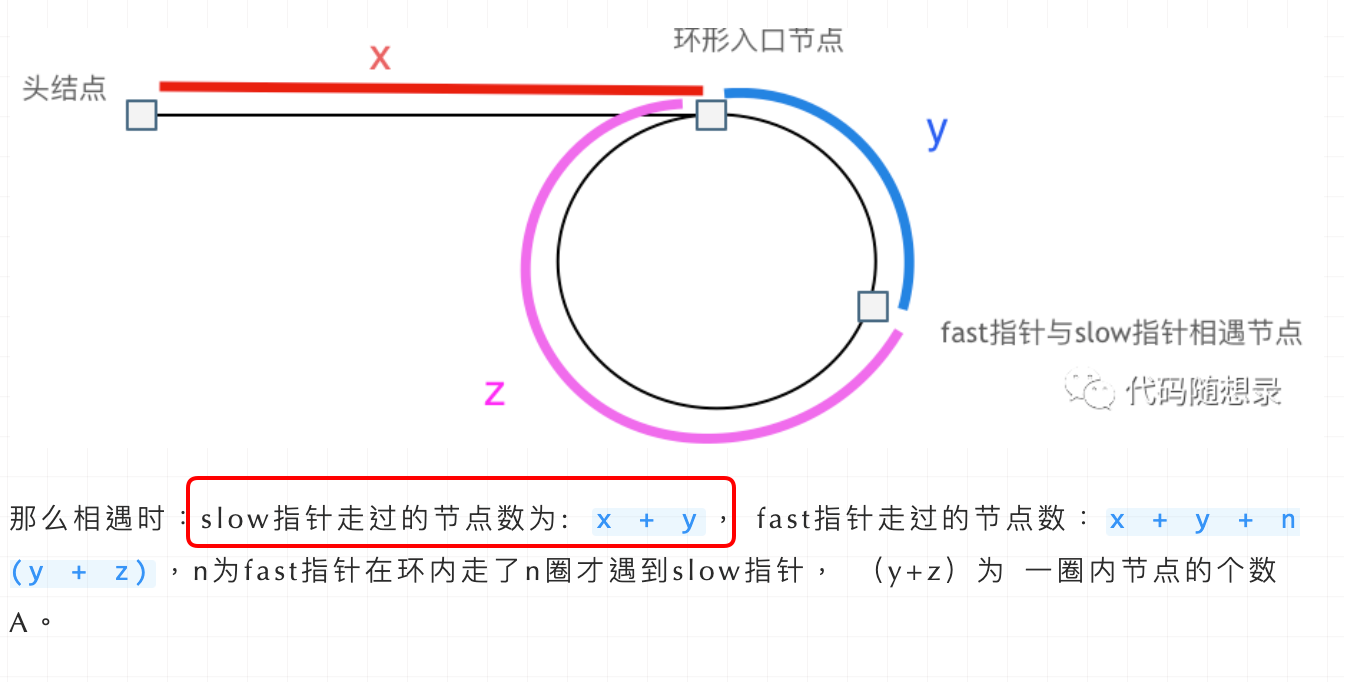
假设链表的头部到环的入口的距离为x，环的入口到快慢指针相遇点的距离为y，相遇点到环的入口的距离为z。

当快慢指针相遇时，慢指针走过的距离是x+y，快指针走过的距离是x+y+n(z+y)。因为快指针的速度是慢指针的两倍，所以2*(x+y) = x+y+n(z+y)，先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。当 n为1的时候解这个等式可以得到x=z。

这就意味着，从链表的头部到环的入口的距离等于从快慢指针相遇点到环的入口的距离。所以，当快慢指针相遇后，我们可以将一个指针移动到链表的头部，然后两个指针同时移动，当它们再次相遇时，就是环的入口。

这就是使用快慢指针可以找到环形链表的数学原理。

var detectCycle = function(head) {
    let slow = head, fast = head;
    while (fast && fast.next) {
        slow = slow.next;
        fast = fast.next.next;
        if (slow === fast) {
            let ptr = head;
            while (ptr !== slow) {
                ptr = ptr.next;
                slow = slow.next;
            }
            return ptr;
        }
    }
    return null;
};