链表相交

好神奇的方法

这段代码是用来找出两个链表的交点的。它使用了两个指针 pA 和 pB，分别从链表 headA 和 headB 的头部开始遍历。

在每一步，pA 和 pB 都会向前移动一步。如果 pA 到达了链表 headA 的末尾，那么将它重置到链表 headB 的头部；同样，如果 pB 到达了链表 headB 的末尾，那么将它重置到链表 headA 的头部。

这样，pA 和 pB 就会同时遍历两个链表。如果两个链表有交点，那么 pA 和 pB 就会在交点处相遇，此时 pA === pB，循环结束，返回 pA（或 pB）即可。如果两个链表没有交点，那么 pA 和 pB 就会同时到达两个链表的末尾，此时 pA === pB === null，循环结束，返回 pA（或 pB，此时为 null）。

这个算法的时间复杂度是 O(N)，空间复杂度是 O(1)，其中 N 是两个链表的总长度。

这个规律的关键在于，当两个链表的长度不同时，通过将指针在到达链表末尾后切换到另一个链表的头部，可以消除长度差异。

假设链表A的长度为a+c，链表B的长度为b+c，其中c是两个链表共享的部分的长度。当我们从链表A的头部和链表B的头部同时开始遍历，到达各自链表末尾时，我们已经遍历了a+c和b+c个节点。此时，如果我们将指针切换到另一个链表的头部继续遍历，那么当两个指针相遇时，它们都已经遍历了a+b+c个节点。

因此，无论两个链表的长度如何，当两个指针相遇时，它们都已经遍历了相同数量的节点。如果两个链表有交点，那么这个交点就是两个指针的相遇点；如果两个链表没有交点，那么两个指针就会在遍历了a+b+c个节点后同时到达链表的末尾，此时pA和pB都为null，循环结束。

这就是为什么这个规律可以找出两个链表的交点，或者确定两个链表没有交点的原因

var getIntersectionNode = function(headA, headB) {
  let pA = headA, pB = headB;
  while(pA !== pB){
    pA = pA === null ? headB : pA.next;
    pB = pB === null ? headA : pB.next;
  }
  return pA;
};

复杂度更高的方法

• 首先确定两个链表的长度

• 对齐：这个过程用图片示意如下；较短的那个位置是关键。
  

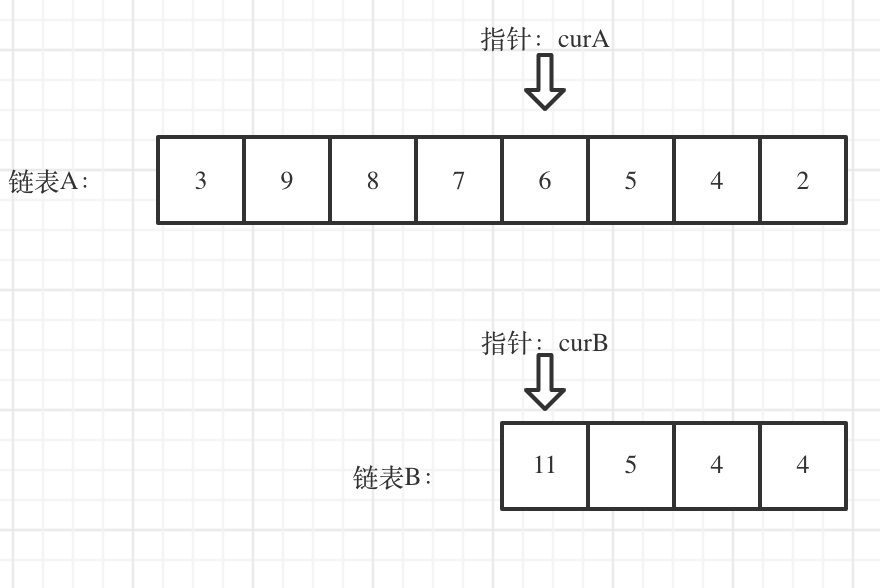
• 找到相同的结点返回即可

var getIntersectionNode = function(headA, headB) {
  var getListLen = (head) => {
    let len = 0;
    while (head) {
      head = head.next;
      len++;
  }
  return len;
  }
  let lenA = getListLen(headA);
  let lenB = getListLen(headB);
  if(lenA>lenB){
    for(let i = 0; i < lenA-lenB; i++){
      headA = headA.next;
    }
  }
  else{
    for(let i = 0; i < lenB-lenA; i++){
      headB = headB.next;
    }
  }
  while(headA){
    if(headA === headB){
      return headA;
    }
    headA = headA.next;
    headB = headB.next;
};
  return null;
}