KMP算法

发表于2024-05-24更新于2024-05-25

KMP算法

非常完整的思路https://www.programmercarl.com/0028.%E5%AE%9E%E7%8E%B0strStr.html#%E6%80%9D%E8%B7%AF

三位学者发明的：Knuth，Morris和Pratt，所以取了三位学者名字的首字母。所以叫做KMP

图 1

用途

KMP主要应用在字符串匹配上。

KMP的主要思想是当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

所以如何记录已经匹配的文本内容，是KMP的重点，也是next数组肩负的重任。

为什么要用前缀表

什么是前后缀

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；

后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串。

最长相等前后缀

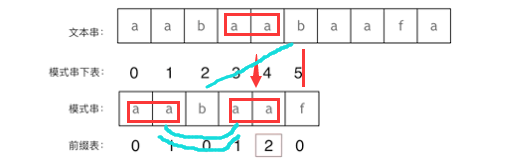
首先要了解文本字符串和模式字符串，前者是题目中提到的haystack，后者是needle。eg:’aabaabaaf’，’aabaaf’

前缀表可以告诉我们应该跳转到哪里继续匹配。而不是从模式字符串的头部重新开始匹配。

图 0

为什么到下表为5时b!=f，可以直接将模式字符串下标调整到2呢。因为最长前后缀相等。
图 1

next实现过程

图 3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const getNext = (nextArr, s) => {
    let j = 0 //i表示后缀末尾，j表示前缀末尾
    nextArr[0] = 0
    for (let i = 1; i < s.length; i++) {
      //什么情况下要向左移动j
      while (s[i] != s[j] && j > 0) {
        j = nextArr[j - 1]
      }
      if (s[i] == s[j]) {
        j++
      }
      nextArr[i] = j
    }
    return nextArr
  }

使用next前缀表实现字符串匹配

图 4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var strStr = function(haystack, needle) {
  const getNext = (nextArr, s) => {
    let j = 0 //i表示后缀末尾，j表示前缀末尾
    nextArr[0] = 0
    for (let i = 1; i < s.length; i++) {
      while (s[i] != s[j] && j > 0) {
        j = nextArr[j - 1]
      }
      if (s[i] == s[j]) {
        j++
      }
      nextArr[i] = j
    }
    return nextArr
  }
  let Arr = new Array(needle.length)
  let nextArr = getNext(Arr,needle)
  let j=0
  //使用next数组实现匹配的过程
  for(let i=0;i<haystack.length;i++){
    //j跳跃的条件
    while(j>0 && j<needle.length && haystack[i] != needle[j]){
      j=nextArr[j-1]
    }
    if(haystack[i] == needle[j]){
      j++
    }
    // 找到匹配字符串的条件
    if( j == needle.length){
      return i-j+1
    }
  }
  return -1
}

重复的子字符串

https://leetcode.cn/problems/repeated-substring-pattern/description/

图 2

思路1

s+s去掉头和尾，如果s还能出现在其中说明符合题目要求。

1
2
3
4
5
6
7
8
9
10
var repeatedSubstringPattern = function (s) {
  let ss = s + s
  ss = ss.slice(1, ss.length)
  ss = ss.slice(0, ss.length - 1)
  if (ss.includes(s)) {
    return true
  } else {
    return false
  }
}

思路2

kmp算法，s.length - 最长相等前后缀，表示重复字符串的长度。

如果能被s.length整除，说明符合条件。

当然如果最长相等前后缀为0，纳智捷说明不符合要求。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
var repeatedSubstringPattern = function(s) {
  //最长相等前后缀
  let nextArr = new Array(s.length)
  nextArr[0] = 0
  let j = 0
  for (let i = 1; i < s.length; i++) {
    while (j > 0 && s[i] != s[j]) {
      j = nextArr[j - 1]
    }
    if (s[i] == s[j]) {
      j++
    }
    nextArr[i] = j
  }
  //先判断nextArr[nextArr.length - 1] != 0是重要的
  // 因为没有最长公共前后缀一定不符合题目要求。

  if (
    nextArr[nextArr.length - 1] != 0 &&
    s.length % (s.length - nextArr[nextArr.length - 1]) === 0
  ) {
    return true
  } else {
    return false
  }
};