动态规划

动态规划基础

动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

动态规划五部曲

• 1、dp数组及其下标得含义
• 2、递推公式
• 3、dp数组如何初始化呢
• 4、遍历顺序
• 5、打印dp数组，为了查错。

基础题目

斐波那契数

https://leetcode.cn/problems/fibonacci-number/description/

思路

• 1、dp数组表示什么，dp[i]：第i个斐波那契数的数值
• 2、递推公式：dp[i] = dp[i-2] + dp[i-1]
• 3、dp数组初始化：dp[0] = 1,dp[1] = 1
• 4、遍历顺序：i从2遍历到n

var fib = function (n) {
  let dp = new Array(n)
  dp[0] = 0
  dp[1] = 1
  if (n == 0) return 0
  if (n == 1) return 1
  if (n > 1) {
    for (let i = 2; i <= n; i++) {
      dp[i] = dp[i - 1] + dp[i - 2]
    }
    return dp[n]
  }
}

爬楼梯

https://leetcode.cn/problems/climbing-stairs/description/

五部曲解释
1、dp数组表示的是，到达第i+1个台阶的方法数
2、递推公式dp[i] = dp[i-2] + dp[i-1]
3、dp数组初始化，dp[0] = 1,dp[1] = 2; 上一个台阶一种方法，两个台阶两种方法
4、遍历顺序从2~n-1

var climbStairs = function(n) {
  let dp=[]
  dp[0] = 1
  dp[1] = 2
  for(let i=2;i<n;i++){
    dp[i] = dp[i-1]+dp[i-2]
  }
  return dp[n-1]
};

使用最小花费爬楼梯

https://leetcode.cn/problems/min-cost-climbing-stairs/description/

五部曲
1、dp数组，代表到达位置i时消耗的花费
2、递推公式 dp[i] = dp[i-1]+cost[i-1]或者dp[i] = dp[i-2]+cost[i-2]，
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3、初始化，dp[0]=0;dp[1]=0，因为题意明确到达台阶不想上跳是没有花费的。而dp数组的含义是到达位置i的花费，所以dp[0]，dp[1]初始化都是0
4、遍历：n是cost长度，顶部在n+1的位置

var minCostClimbingStairs = function(cost) {
  let dp = []
  dp[0]=0,dp[1]=0;
  n = cost.length
  for(let i=2;i<=n;i++){
    dp[i] = Math.min(dp[i-1] + cost[i-1],dp[i-2] + cost[i-2])
  }
  return dp[n]
};

不同路径

https://leetcode.cn/problems/unique-paths/description/

五部曲
1、dp[i][j],从0，0，走到i，j的走法。
2、dp[i][j] = dp[i-1][j] + dp[i][j-1]
3、初始化：dp[0][j] = 1;dp[i][0] = 1
4、遍历：
5、

var uniquePaths = function (m, n) {
  let dp = Array(m).fill().map(() => Array(n).fill(0))
  dp[0][0] = 1
  for (let i = 0; i < m; i++) dp[i][0] = 1
  for (let i = 0; i < n; i++) dp[0][i] = 1
  for (let i = 1; i < m; i++) {
    for (let j = 1; j < n; j++) {
      dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
    }
  }
  return dp[m - 1][n - 1]
}

不同路径II

https://leetcode.cn/problems/unique-paths-ii/description/

有障碍物的地方路径数量设为0即可解决

五部曲
1、dp数组及下标含义：dp[i][j]表示到达i，j的路径数量
2、递推公式：如果i，j处有障碍，dp[i][j]=0，没有障碍dp[i][j] = dp[i-1][j] + dp[i][j-1]
3、初始化,dp数组全部填充为0，dp[0][0] = 1
4、遍历方法，i:0~m j:0~n,这种遍历方式要搭配if(i > 0) dp[i][j] += dp[i-1][j];
if(j > 0) dp[i][j] += dp[i][j-1];

var uniquePathsWithObstacles = function(obstacleGrid) {
  const m = obstacleGrid.length,n=obstacleGrid[0].length
  let dp = Array(m).fill().map(() => Array(n).fill(0))
  dp[0][0]=1
  for(let i=0;i<m;i++){
    for(let j=0;j<n;j++){
      if (obstacleGrid[i][j] == 1) dp[i][j]=0
      else{
       if(i > 0) dp[i][j] += dp[i-1][j];
       if(j > 0) dp[i][j] += dp[i][j-1];
      }
    }
  }
  return dp[m-1][n-1]
};

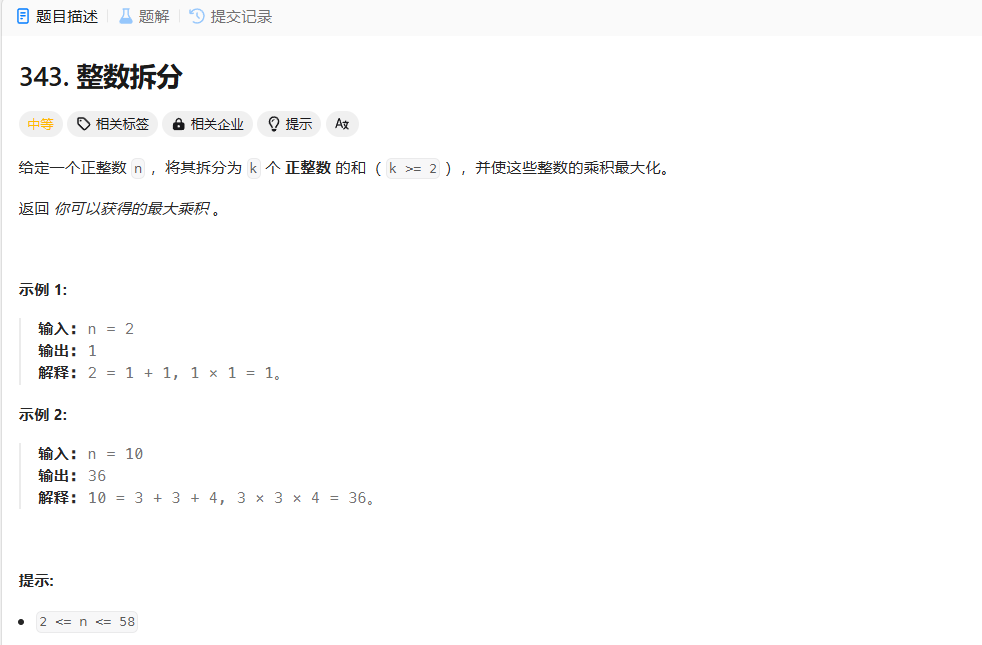
整数拆分

https://leetcode.cn/problems/integer-break/description/

五部曲
1、dp数组及其下标的含义：dp[i]表示i拆分的最大值。
2、递推公式：

3、初始化：dp[2] = 1,其余均为0
4、遍历顺序：按顺序拆，一定拆出1，拆能两个数和多个数；一定拆除2，拆出两个数和多个数…，求每一次拆的最大值。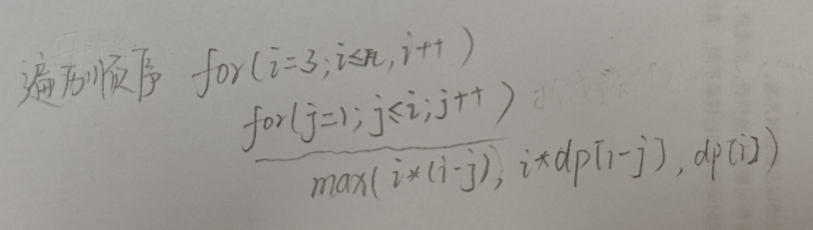

var integerBreak = function(n) {
  let dp = Array(n+1).fill(0)  //n+1因为dp数组下标的含义
  dp[2]=1
  for(let i=0;i<=n;i++){
    for(let j=1;j<= Math.floor(i/2);j++){
      dp[i] = Math.max(j*(i-j),j*dp[i-j],dp[i])
    }
  }
  return dp[n]
};

不同的二叉搜索树

https://leetcode.cn/problems/unique-binary-search-trees/description/

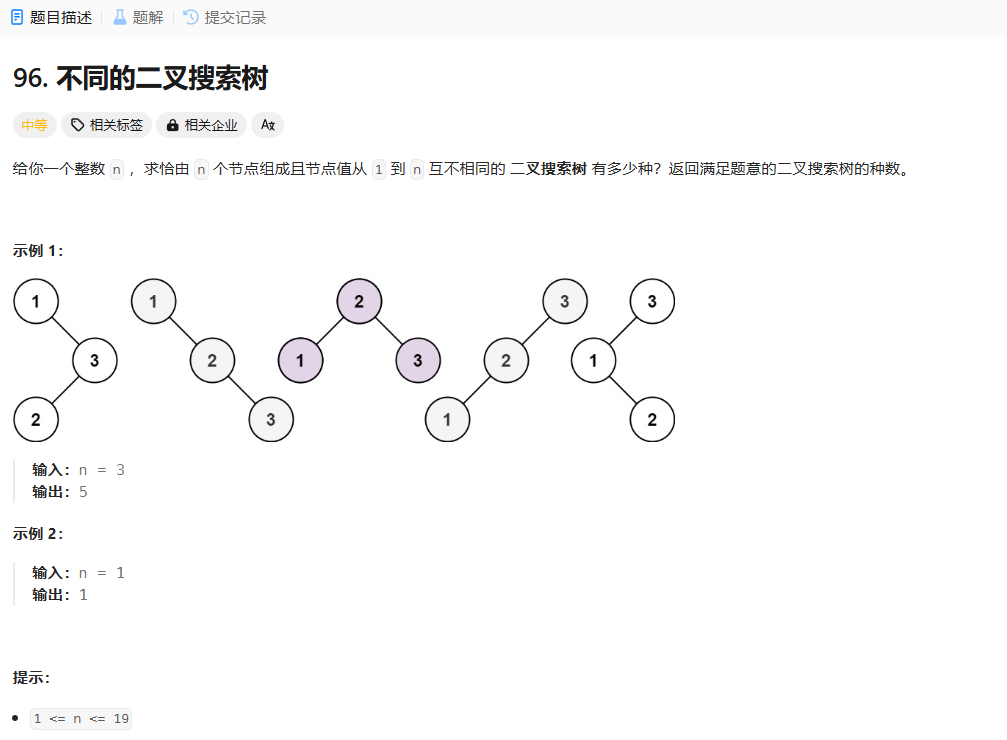
二叉搜索树

五部曲
1、dp[i] 表示i个结点的二叉搜索数的个数
2、递推公式:dp[i] += dp[j-1] * dp[i-j]
当头结点为j时，左边一定有j-1个结点。

3、初始化：dp[0] = 1, dp[1] = 1, dp[2]=2
4、遍历顺序，第一层for循环负责遍历dp[i]的下标，第二个for循环遍历头节点的数值

var numTrees = function(n) {
  let dp = Array(n+1).fill(0)
  dp[0]=1,dp[1]=1,dp[2]=2
  for(let i=3;i<=n;i++){
    for(let j=1;j<=i;j++){
      dp[i] += dp[j-1]*dp[i-j]
    }
  }
  return dp[n]
};