01背包

背包问题

背包分类

01背包

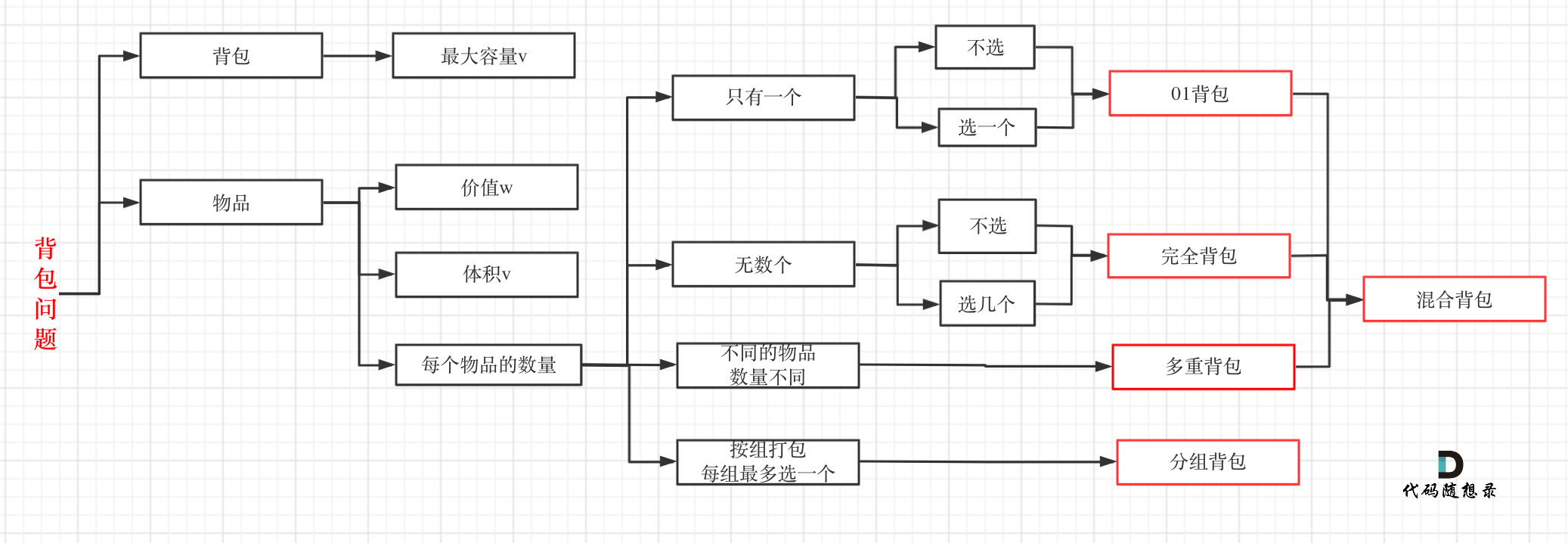
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

二维dp数组

五部曲
1、二维dp数组，dp[i][j]，i表示物品的编号，j表示背包重量，存储值表示价值
dp[i][j] 表示从0-i的物品中拿总重量<=j的物品的最高价值。
2、递推公式:if j-weight[i] >= 0 dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]) else dp[i][j] = dp[i-1][j]
如果符合条件，那么在拿i与不拿i的较大值中取，如果j小于i的重量，那只有一个选择，选择dp[i-1][j]
3、初始化，dp[i][0] = 0,因为重量为0，能拿0个物品，价值为0
dp[0][i] 的值取决于weight[i]和j，如果 weight[i]<=j , dp[0][i] = value[i] 否则，dp[0][j] = 0
4、遍历 for(let i = 0;i<m;i++){ for(let j=1;j<=n;j++){}}

// js node ACM模式
const readline = require('readline');
const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout
});
const inputArr = [];
rl.on('line',function(line){
    inputArr.push(line.split(' '))
}).on('close',function(){
    const m = parseInt(inputArr[0][0])
    const n = parseInt(inputArr[0][1])
    const weight = inputArr[1].map(Number)
    const bag = inputArr[2].map(Number)
    let dp = Array(m).fill().map(()=> Array(n+1).fill(0))
    for(let i=0;i<m;i++){
        for(let j=1;j<=n;j++){
            if (i==0){
                if(j>=weight[i]) dp[i][j]=bag[i]
            }
            else{
                // 两种情况
                if(j-weight[i]>=0) dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-weight[i]]+bag[i])
                else dp[i][j]  = dp[i-1][j]
            }
        }
    }
    console.log(dp[m-1][n])
})

一维dp数组（滚动数组）

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

倒序遍历的原因：dp[j]的状态受dp[0~j-1]的状态的影响，因此需要倒序遍历。

const readline = require('readline')

const rl = readline.createInterface({
    input: process.stdin,
    output: process.stdout
})

inputArr = []
rl.on('line',function(line){
    inputArr.push(line.split(' '))
}).on('close',function(){
    const m = parseInt(inputArr[0][0])
    const n = parseInt(inputArr[0][1])
    const mArr = inputArr[1].map(Number)
    const vArr = inputArr[2].map(Number)
    let dp = Array(n+1).fill(0)
    for(let i=0;i<m;i++){
        for(let j=n;j>=mArr[i];j--){
            dp[j] = Math.max(dp[j],dp[j-mArr[i]]+vArr[i])
        }
    }
    console.log(dp[n])
})

题目

分割等和子集416

https://leetcode.cn/problems/partition-equal-subset-sum/description/

思路
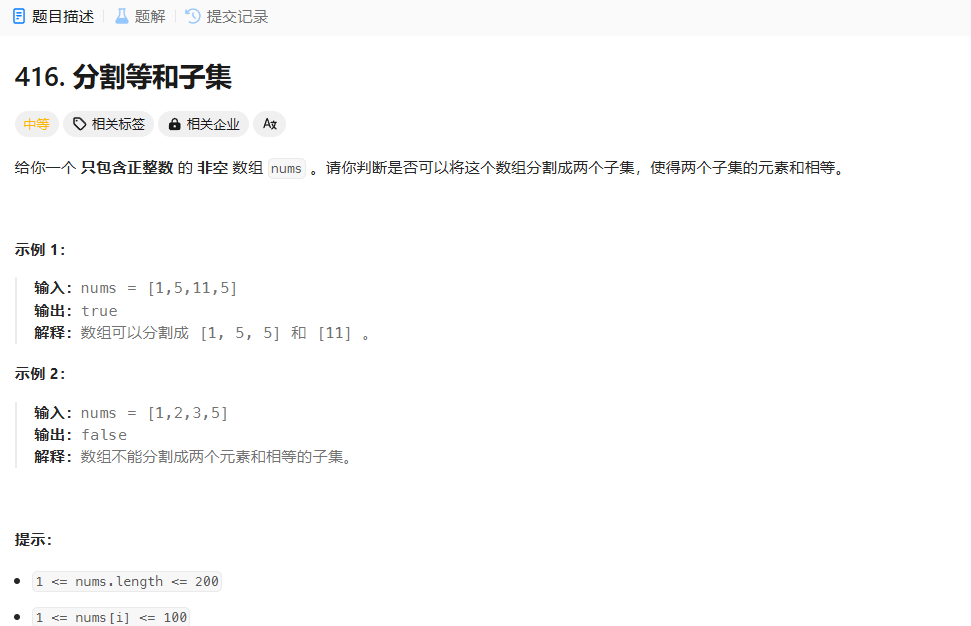
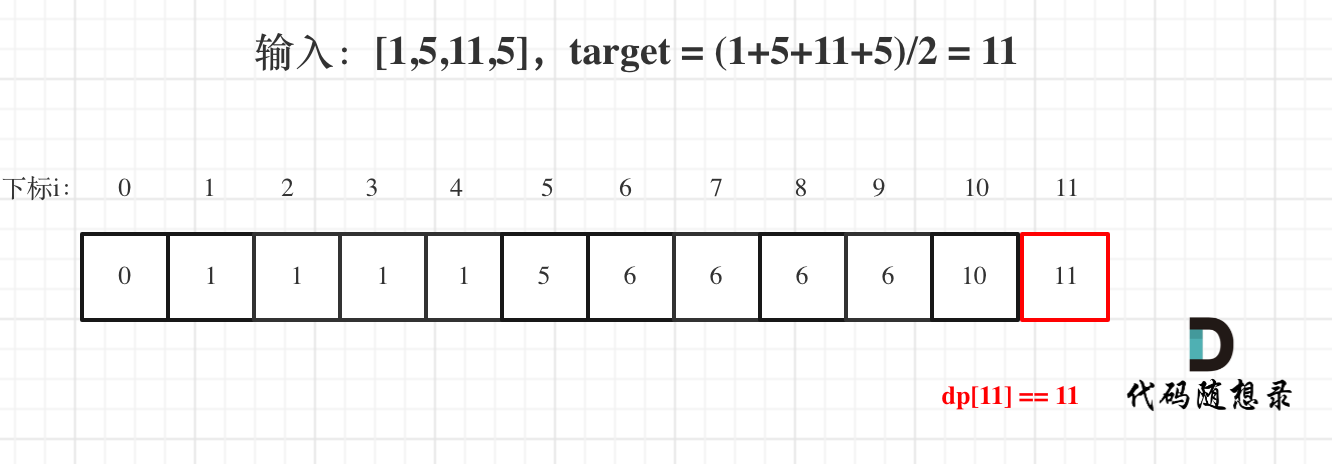
分成两个和相等的数组，只要有一个子集满足 sum(arr)/2 即可

这里没有价值，以物品重量为价值，weight = value 背包装满到数组和的二分之一时，价值达到同样的值就算是成功了。
dp[target] = target

五部曲
1、dp[j] 含义，容量为j的背包所能装的最大价值
2、递推公式，dp[j] = max(dp[j],dp[j-nums[i]])
3、初始化：dp = [0,0,0,…]
4、遍历物品i正序，背包容量j逆序。

var canPartition = function(nums) {
  // 数组求和
  let sum= nums.reduce((acc, val) => acc + val, 0)
  // sum如果是偶数可以继续，如果是奇数直接返回false
  if (sum%2 != 0) return false
  let target = sum/2
  let dp = Array(target+1).fill(0)
  for(let i=0;i<nums.length;i++){
    for(let j=target;j>=nums[i];j--){
      dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i])
    }
  }
  if (dp[target]==target) return true
  return false
};

最后一块石头的重量 II

https://leetcode.cn/problems/last-stone-weight-ii/description/

思路
将石头分为两组，并尽可能使得两组石头重量尽可能相等
最后剩余石头的重量 = 数组1总和 - 数组2总和
let target = Math.floor(sum/2), 由于向下取整target<= sum-target, sum - dp[target] >= dp[target]

五部曲
1、dp[j],表示石头放入容量为j的背包能达到的最大重量。
2、递推公式：dp[j] = Math.max(dp[j],dp[j-stones[i]+stones[i]])
3、初始化：dp[0] = 0，背包容量为0时能放的重量为0，其余位置也时0，因为递推公式是求最大值。石头的重量是正数，因此初始化为0，不影响结果。
4、遍历顺序：石头正序，背包重量逆序

var lastStoneWeightII = function(stones) {
  let sum = stones.reduce((acc,val)=> acc+val,0)
  let target = Math.floor(sum/2)
  let dp = Array(target+1).fill(0)
  for(let i=0;i<stones.length;i++){
    for(let j=target;j>=stones[i];j--){
      dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i])
    }
  }
  return sum-dp[target]-dp[target]
};

目标和

https://leetcode.cn/problems/target-sum/description/

思路
讲确定两个数组的问题转换化简为确定一个数组，
把整个数组可以被分成两个子数组，两个子数组中数字和分别为left和right，则有
left - right = target
left + right = sum
可推导出：left - sum + left = target; left = (sum + target)/2
问题转换为组合和为left的问题，可以用回溯暴力破解。

这个问题转换为背包问题是求，装满容量为j的背包的方法。

五部曲
1、dp[j]表示装满容量为j的背包的方法数
2、递推公式：dp[j] = dp[j-nums[i]],
数组为[1,2,3,4,5]
eg：dp[5] = dp[4] + dp[3] + dp[2] + dp[1] + dp[0]
3、初始化：dp[0] = 1
4、遍历顺序：外层遍历数组（正序），内层遍历背包容量（倒序）

var findTargetSumWays = function(nums, target) {
  let sum = nums.reduce((acc,val)=>acc+val,0)
  if (Math.abs(target) > sum)  return 0
  if ((sum + target) % 2 == 1) return 0
  let left = (sum + target)/2
  let dp = Array(left+1).fill(0)
  dp[0] = 1
  for (let i=0; i<nums.length; i++){
    for(let j=left;j>=nums[i];j--){
      dp[j] += dp[j-nums[i]]
    }
  }
  return dp[left]
};

一和零

https://leetcode.cn/problems/ones-and-zeroes/description/

背包容量发生一些变化的01背包，背包容量分为两部分，m用于存储0，n用于存储1

五部曲
1、dp[i][j] 表示0容量为i，1容量为j的背包所能存放的字符串的数量。
2、递推公式：max(dp[i][j],dp[i-zeroNum][j-oneNum]+1); 实际上每一行是一个一维滚动数组
3、初始化：都初始化为0
4、遍历顺序：物品正序，ij逆序。因为是滚动数组

var findMaxForm = function(strs, m, n) {
  let dp = Array.from(Array(m+1), () => Array(n+1).fill(0));
  for (let str of strs) {
    let zeroNum = 0, oneNum = 0;
    for (let s of str) {
      if (s === '1') oneNum++;
      else zeroNum++;
    }
    for(let i = m; i >= zeroNum; i--) {
      for (let j = n; j >= oneNum; j--) {
        dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
      }
    }
  }
  return dp[m][n];
};

多重背包

https://kamacoder.com/problempage.php?pid=1066

let readline = require('readline')
const rl = readline.createInterface({
    input:process.stdin,
    output:process.stdout99
})
let inputArr = []
rl.on('line',function(line){
    inputArr.push(line.split(' '))
}).on('close',function(){
    let n = parseInt(inputArr[0][0])
    let m = parseInt(inputArr[0][1])
    let w = inputArr[1].map(Number)
    let v = inputArr[2].map(Number)
    let num = inputArr[3].map(Number)
    let dp = Array(n+1).fill(0)
    //遍历物品
    for (let i=0;i<m;i++){
      //背包
        for(let j = n;j>=w[i];j--){
            for(let k=1;k<=num[i] && k*w[i]<=j;k++){
                dp[j] = Math.max(dp[j],dp[j-w[i]*k]+v[i]*k)
            }
        }
    }
    console.log(dp[n])
})