子序列与动态规划问题

最长递增子序列

https://leetcode.cn/problems/longest-increasing-subsequence/description/

图 0

思路
本题也是代码随想录中子序列问题的第一题，如果没接触过这种题目的话，本题还是很难的，甚至想暴力去搜索也不知道怎么搜。子序列问题是动态规划解决的经典问题，当前下标i的递增子序列长度，其实和i之前的下表j的子序列长度有关系，那又是什么样的关系呢。

1、dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
为什么一定表示 “以nums[i]结尾的最长递增子序” ，因为我们在做递增比较的时候，如果比较 nums[j] 和 nums[i] 的大小，那么两个递增子序列一定分别以nums[j]为结尾和 nums[i]为结尾，要不然这个比较就没有意义了，不是尾部元素的比较那么如何算递增呢。
2、状态转移方程
- if (nums[i]>nums[j]) dp[i] = max(dp[i],dp[j]+1)这里的含义是，取dp[j]+1的最大值。
3、初始化，子序列的长度最短为1
4、遍历顺序，外层遍历i(1 ~ n)，内层遍历j(0 ~ i-1)
还要注意并不是dp[n-1]才是最终的值，最大值应该是dp数组中的最大值。

var lengthOfLIS = function(nums) {
  let n = nums.length
  let dp = Array(n).fill(1)
  let result = 1
  for(let i=1;i<n;i++){
    for(let j=0;j<i;j++){
      if (nums[i]>nums[j]) dp[i] = Math.max(dp[i],dp[j]+1)
    }
    if (dp[i]>result) result = dp[i]
  }
  return result
};

最长递增子序列

https://leetcode.cn/problems/longest-continuous-increasing-subsequence/description/

图 1

思路
这里的序列要连续，因此当前的状态要由前一个决定

1、dp[i]：以下标i为结尾的连续递增的子序列长度为dp[i]
2、if(nums[i]>nums[i-1]) dp[i] = dp[i-1]+1
3、初始化dp[i]都等于1
4、循环，只需要一层循环遍历i即可
当然同样注意最终答案不是dp[n-1]，而是dp数组中的最大值

var findLengthOfLCIS = function(nums) {
  let n = nums.length
  let dp = Array(n).fill(1)
  let result =1
  for(let i=1;i<n;i++){
    if(nums[i]>nums[i-1]) dp[i] = dp[i-1]+1
    if (dp[i]>result) result = dp[i]
  }
  return result
};

最长重复子数组

https://leetcode.cn/problems/maximum-length-of-repeated-subarray/description/

图 2

难点
动态数组怎么表示，又是什么含义

思路
如果要暴力破解的话，把每个数组的子数组遍历出来，然后两两比较，得出最长重复子数组

1、二维dp[i][j]，以i-1为结尾的nums[1]和以j-1为结尾的nums[2],的最长重复子数组的长度；本质上也是两两比较了，但是由于我记录了前一个状态的值，在进行下一个状态比较时，子需要对比一个数即可结合前一个状态得出现在状态的值。
- 为什么i，j表示下标为i-1和j-1呢？因为有dp[i-1],dp[j-1],因此i和j的最小值应该为1。dp数组遍历时候从1开始，但是nums数组要从0号元素开始比较。
2、递推公式：if(nums[i-1]==nums[j-1]) dp[i][j] = dp[i-1][j-1] +1;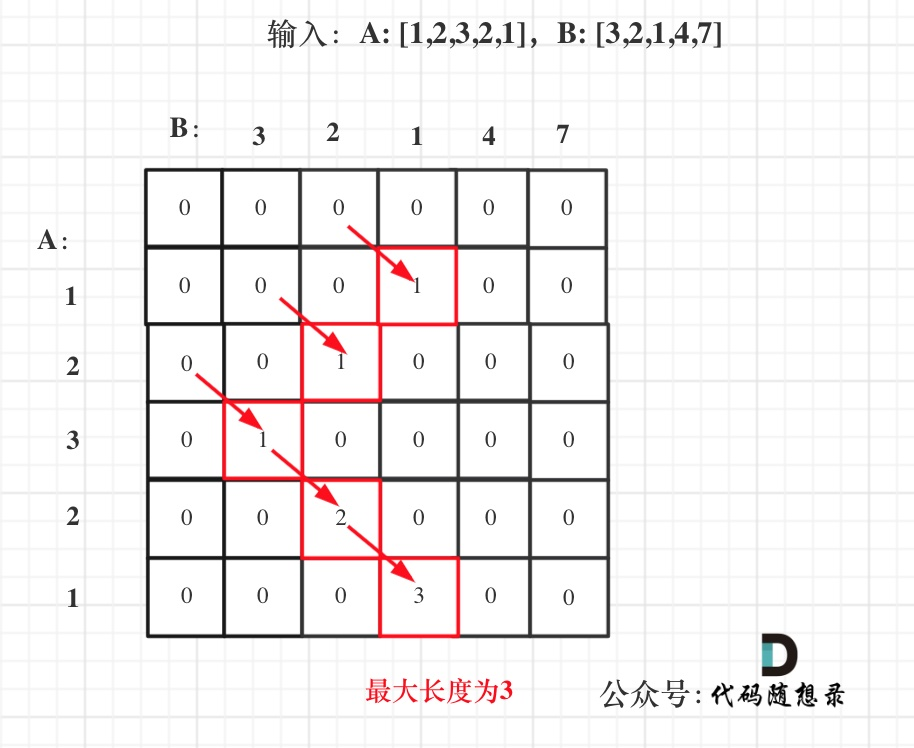
3、初始化：dp[i][0] = 0,dp[0][j] = 0;因为i和j遍历时都从1开始
4、遍历顺序：
这题也是结果在过程中，而不是遍历完之后。

var findLength = function(nums1, nums2) {
  let n = nums1.length
  let m = nums2.length
  let dp = Array.from({length:n+1},()=>Array(m+1).fill(0))
  let result = 0
  for (let i=1;i<=n;i++){
    for(let j=1;j<=m;j++){
      if(nums1[i-1] == nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1
      if (dp[i][j] > result) result = dp[i][j]
    }
  }
  return result
};

最长公共子序列

https://leetcode.cn/problems/longest-common-subsequence/description/

图 3

思路
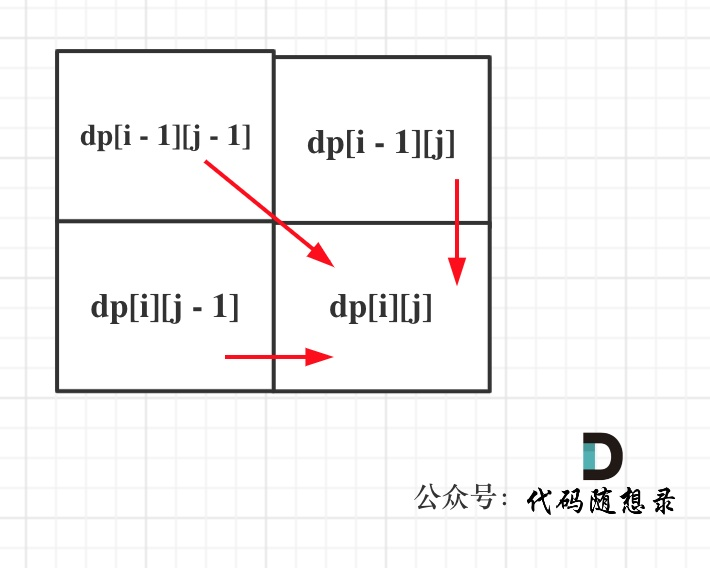
这道题就是可以不连续，可以不连续前面一维数组做过，不过现在dp需要时二维数组，因此这题主要突破点再递推公式上

1、dp[i][j]表示以i-1为结尾的第一个字符串和j-1结尾的第二个字符串的最长公共子序列长度
2、递推公式：主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同。
- if (text1[i-1]==text2[j-1]) dp[i][j] = dp[i-1][j-1]+1;
- else dp[i][j] = max(dp[i-1][j],dp[i][j-1])
3、初始化，均为0即可，
4、遍历顺序，那么为了在递推的过程中，这三个方向都是经过计算的数值，所以要从前向后，从上到下来遍历这个矩阵。

var longestCommonSubsequence = function(text1, text2) {
  let n = text1.length
  let m = text2.length
  let dp = Array.from({length:n+1},()=> Array(m+1).fill(0))
  for(let i=1;i<=n;i++){
    for(let j=1;j<=m;j++){
      if (text1[i-1]==text2[j-1]) dp[i][j] = dp[i-1][j-1]+1
      else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])
    }
  }
  return dp[n][m]
};

不相交的线

https://leetcode.cn/problems/uncrossed-lines/description/

图 2

思路
其实也就是说A和B的最长公共子序列是[1,4]，长度为2。这个公共子序列指的是相对顺序不变（即数字4在字符串A中数字1的后面，那么数字4也应该在字符串B数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

var maxUncrossedLines = function(nums1, nums2) {
  let n = nums1.length
  let m = nums2.length
  let dp = Array.from({length:n+1},()=>Array(m+1).fill(0))
  for(let i = 1;i<=n;i++){
    for(let j = 1;j<=m;j++){
      if (nums1[i-1]==nums2[j-1]) dp[i][j] = dp[i-1][j-1]+1
      else dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])
    }
  }
  return dp[n][m]
};