字母迷宫

发表于2024-07-23更新于2024-07-23

字母迷宫(单词搜索)

图 0

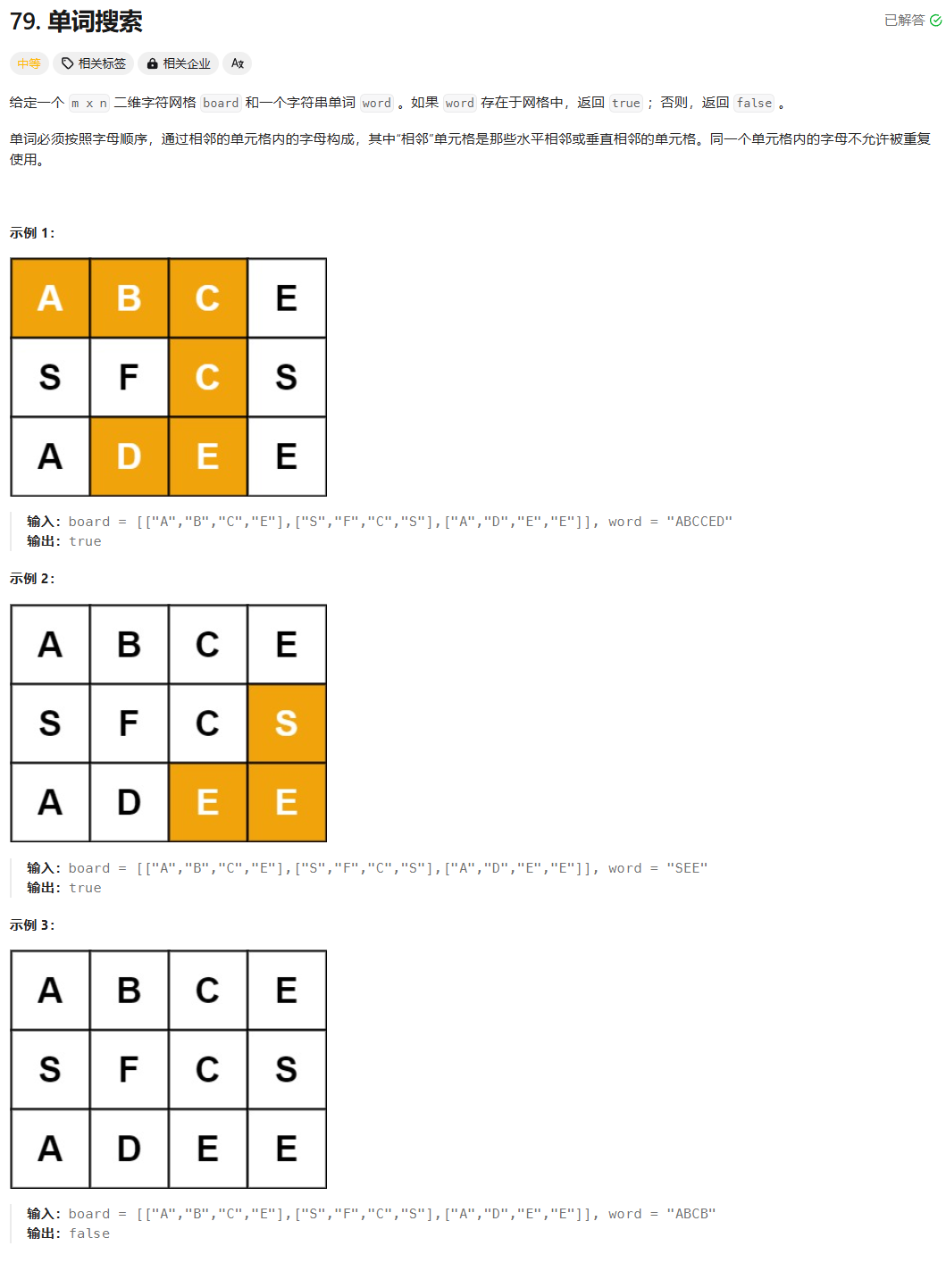
思路

刚开始看到这题，知道用回溯算法，所以回忆了回溯算法三部曲

  • 1、确定参数
  • 2、确定终止条件
  • 3、单层搜索逻辑

但是看了半天之确定了参数，终止条件和单层逻辑都理出来。看了讲解知道了原因。

第一个字母的匹配逻辑和后续字母匹配逻辑不一致。

  • 第一个字母就在矩阵中挨个遍历，哪个元素等于target[0],就可以开始下一个字母。

  • 而非第一个字的匹配，是要在第一个匹配上的字母的上下左右寻找。

前者按照行列遍历，后者按照方向遍历。因此有必要分成两部分，先找到第一个字母吗，然后后续字母遵照一样的逻辑处理。

思路详解

  • 1、参数：i,j,k分别表示矩阵的行、矩阵的列以及当前遍历到target字符的哪一位字符
  • 2、确定终止条件
    • 如果当前位置的字符不等于 target[k]，则当前路径不可能构成目标单词，返回 false。
    • 如果 k == target.length - 1 且当前字符匹配，说明已经成功找到目标单词，返回 true。
    • 注意，还应该有一个终止条件是检查 (i, j) 是否越界或者该位置已经被访问过，以避免重复访问。
  • 3、单层搜索逻辑：
    • 对于矩阵中的每一个元素，如果它是 target[0]，则从这个元素开始，尝试所有可能的搜索路径。
    • 一旦找到匹配的第一个字母，后续的搜索应该限制在当前元素的上下左右四个方向上。
    • 搜索过程中，需要标记当前路径已访问过的位置，以避免循环访问。搜索后，需要撤销标记（回溯），以便其他搜索路径可以使用这些位置。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var wordPuzzle = function(grid, target) {
  const h = grid.length,
    w = grid[0].length;
  const direction = [
    [0, 1],
    [0, -1],
    [1, 0],
    [-1, 0]
  ];
  const visited = Array.from({ length: h }, () => Array(w).fill(false));

  const check = (i, j, k) => {
    if (grid[i][j] != target[k]) return false;
    else if (k == target.length - 1) return true; // 修正比较操作

    visited[i][j] = true;
    //向四分方向寻找
    for (let [dx, dy] of direction) { // 添加let声明
      let newi = i + dx, newj = j + dy;
      if (newi >= 0 && newi < h && newj >= 0 && newj < w && !visited[newi][newj]) { // 修正条件判断
        if (check(newi, newj, k + 1)) {
          return true; // 找到匹配后立即返回true
        }
      }
    }
    visited[i][j] = false;
    return false;
  };
  // 第一个字母的判断
  for (let i = 0; i < h; i++) {
    for (let j = 0; j < w; j++) {
      if (check(i, j, 0)) {
        return true;
      }
    }
  }
  return false;
}

copilot 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var wordPuzzle = function(grid, target) {
  const h = grid.length,
        w = grid[0].length;
  const directions = [
    [0, 1],  // 右
    [0, -1], // 左
    [1, 0],  // 下
    [-1, 0]  // 上
  ];

  const visited = Array.from({ length: h }, () => Array(w).fill(false));

  const dfs = (i, j, k) => {
    if (i < 0 || i >= h || j < 0 || j >= w || visited[i][j] || grid[i][j] !== target[k]) {
      return false;
    }
    if (k === target.length - 1) {
      return true;
    }
    visited[i][j] = true;
    for (const [di, dj] of directions) {
      if (dfs(i + di, j + dj, k + 1)) {
        return true;
      }
    }
    visited[i][j] = false; // 回溯
    return false;
  };

  for (let i = 0; i < h; i++) {
    for (let j = 0; j < w; j++) {
      if (grid[i][j] === target[0] && dfs(i, j, 0)) {
        return true;
      }
    }
  }
  return false;
};