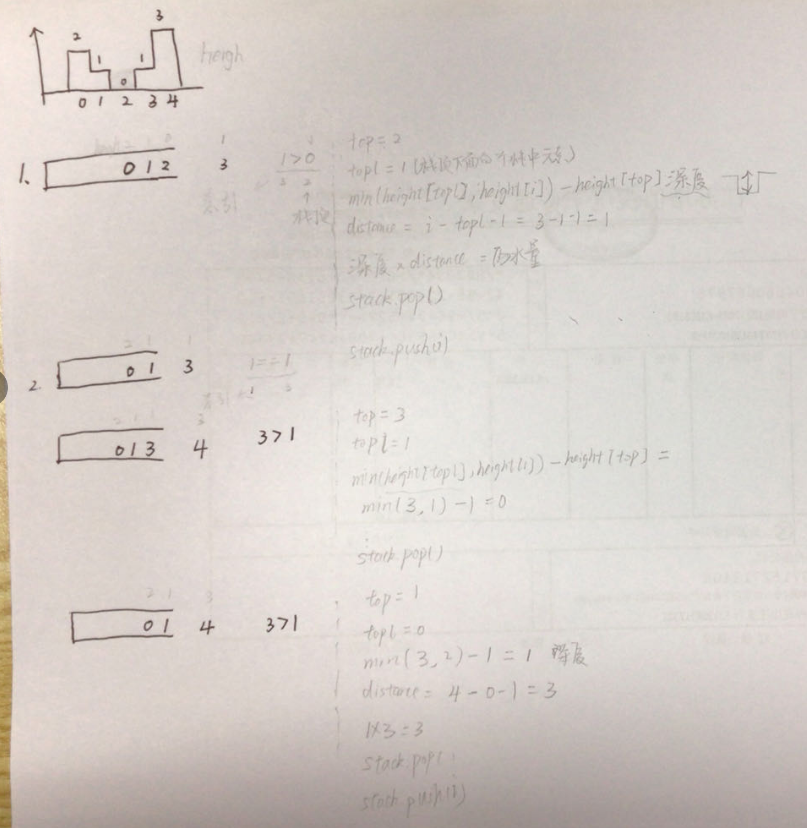
web缓存
是什么
解决的问题与优缺点
- 减少不必要的网络传输,节省带宽。
- 更快加载页面
- 减少服务器负担,避免服务器过载
实际场景:
其实日常的开发中,我们最最最最关心的,还是”更快的加载页面”;尤其是对于react/vue等SPA(单页面)应用来说,首屏加载是老生常谈的问题。这个时候,缓存就显得非常重要。不需要往后端请求,直接在缓存中读取。速度上,会有显著的提升。是一种提升网站性能与用户体验的有效策略。
知识扩展
- 单页Web应用(single page web application,SPA),整个应用在初次加载时加载一个包含必要资源的HTML页面,之后所有的页面内容变化都是通过JavaScript动态更新DOM来实现,不需要重新加载整个页面。
- 多页面应用,每次用户导航到新的页面时,都需要从服务器加载一个新的HTML页面。

强缓存和协商缓存
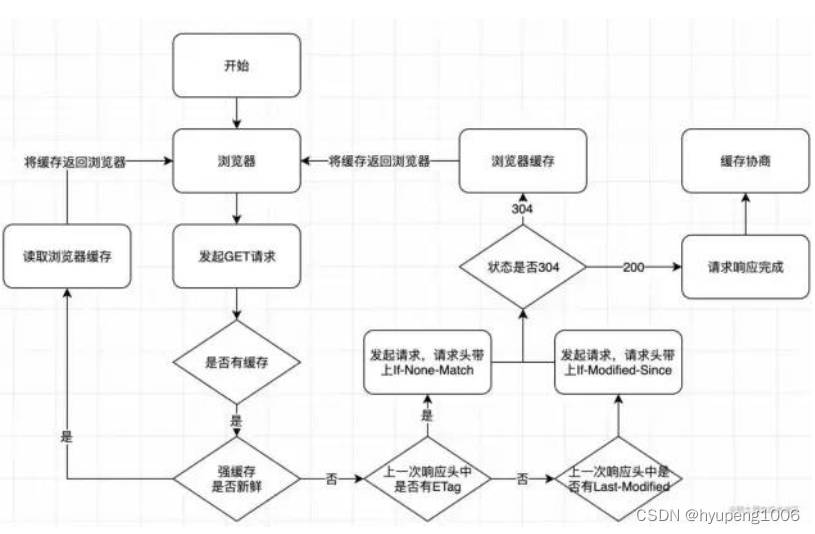
强缓存
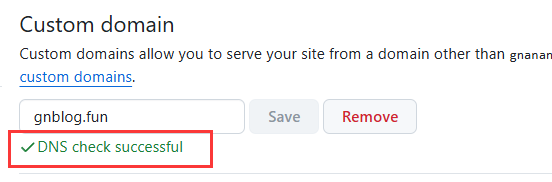
从强制缓存的角度触发,如果浏览器判断请求的目标资源有效命中强缓存,如果命中,则可以直接从内存中读取目标资源,无需与服务器做任何通讯。
Cache-control的使用方法页很简单,只要在资源的响应头上写上需要缓存多久就好了,单位是秒。比如
在响应头中Cache-Control:’max-age=10’
Cache-Control:max-age=N,N就是需要缓存的秒数。从第一次请求资源的时候开始,往后N秒内,资源若再次请求,则直接从磁盘(或内存中读取),不与服务器做任何交互。
- Cache-control有max-age、s-maxage、no-cache、no-store、private、public这六个属性。
- max-age决定客户端资源被缓存多久。
- s-maxage决定代理服务器缓存的时长。
- no-cache表示是强制进行协商缓存。
- no-store是表示禁止任何缓存策略。
- public表示资源即可以被浏览器缓存也可以被代理服务器缓存。
- private表示资源只能被浏览器缓存。
注意,no-cache和no-store是一组互斥属性,这两个属性不能同时出现在Cache-Control中。
注意,public和private也是一组互斥属性。他们两个不能同时出现在响应头的cache-control字段中。
注意,max-age和s-maxage并不互斥。他们可以一起使用。
协商缓存
- 基于last-modified的协商缓存
基于last-modified的协商缓存实现方式是:
1、首先需要在服务器端读出文件修改时间,
2、将读出来的修改时间赋给响应头的last-modified字段。
3、最后设置Cache-control:no-cache
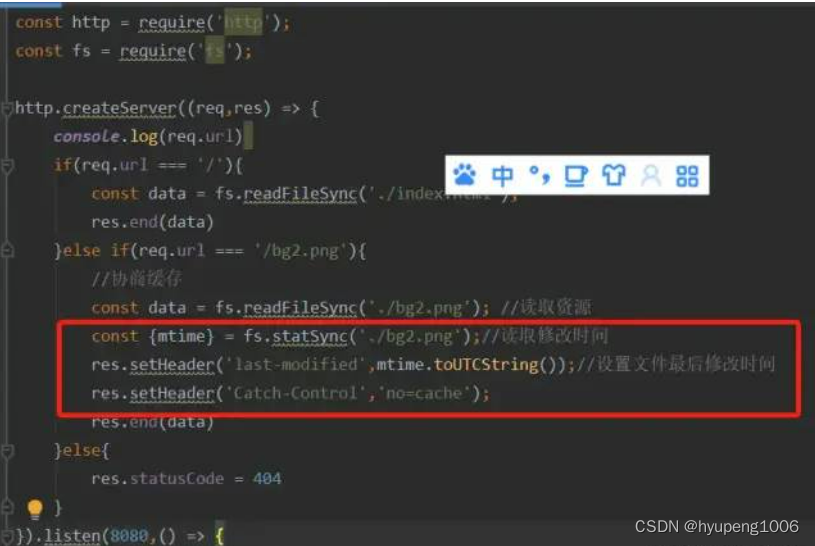
注意圈出来的三行。
第一行,读出修改时间。
第二行,给该资源响应头的last-modified字段赋值修改时间
第三行,给该资源响应头的Cache-Control字段值设置为:no-cache.(上文有介绍,Cache-control:no-cache的意思是跳过强缓存校验,直接进行协商缓存。)
还没完。到这里还无法实现协商缓存
当客户端读取到last-modified的时候,会在下次的请求标头中携带一个字段:If-Modified-Since。
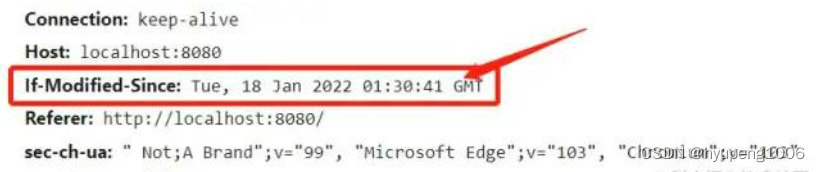
那么之后每次对该资源的请求,都会带上If-Modified-Since这个字段,而务端就需要拿到这个时间并再次读取该资源的修改时间,让他们两个做一个比对来决定是读取缓存还是返回新的资源。
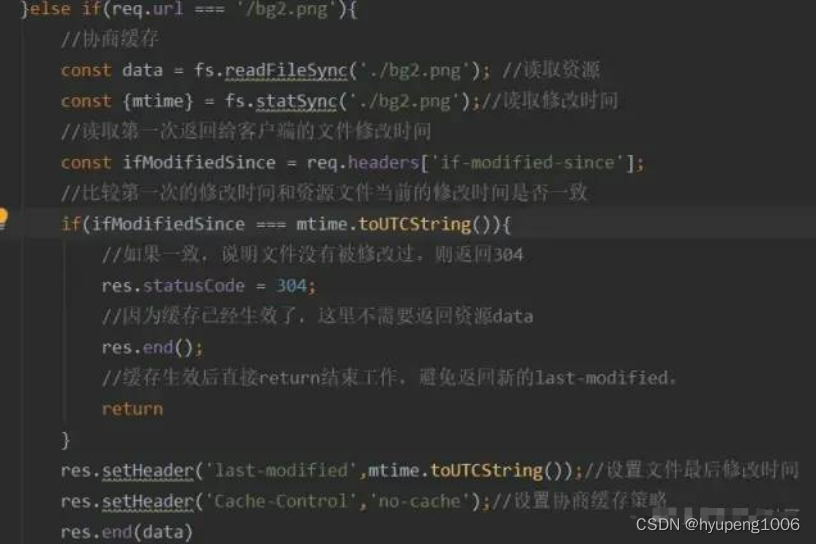
使用以上方式的协商缓存已经存在两个非常明显的漏洞。这两个漏洞都是基于文件是通过比较修改时间来判断是否更改而产生的。
1.因为是更具文件修改时间来判断的,所以,在文件内容本身不修改的情况下,依然有可能更新文件修改时间(比如修改文件名再改回来),这样,就有可能文件内容明明没有修改,但是缓存依然失效了。
2.当文件在极短时间内完成修改的时候(比如几百毫秒)。因为文件修改时间记录的最小单位是秒,所以,如果文件在几百毫秒内完成修改的话,文件修改时间不会改变,这样,即使文件内容修改了,依然不会 返回新的文件。
为了解决上述的这两个问题。从http1.1开始新增了一个头信息,ETag(Entity 实体标签)
基础ETag的协商缓存
不用太担心,如果你已经理解了上面比较时间戳形式的协商缓存的话,ETag对你来说不会有难度。
ETag就是将原先协商缓存的比较时间戳的形式修改成了比较文件指纹。
文件指纹:根据文件内容计算出的唯一哈希值。文件内容一旦改变则指纹改变。
1.第一次请求某资源的时候,服务端读取文件并计算出文件指纹,将文件指纹放在响应头的etag字段中跟资源一起返回给客户端。
2.第二次请求某资源的时候,客户端自动从缓存中读取出上一次服务端返回的ETag也就是文件指纹。并赋给请求头的if-None-Match字段,让上一次的文件指纹跟随请求一起回到服务端。
3.服务端拿到请求头中的is-None-Match字段值(也就是上一次的文件指纹),并再次读取目标资源并生成文件指纹,两个指纹做对比。如果两个文件指纹完全吻合,说明文件没有被改变,则直接返回304状态码和一个空的响应体并return。如果两个文件指纹不吻合,则说明文件被更改,那么将新的文件指纹重新存储到响应头的ETag中并返回给客户端