分发饼干

策略:size大的饼干给胃口大的小孩。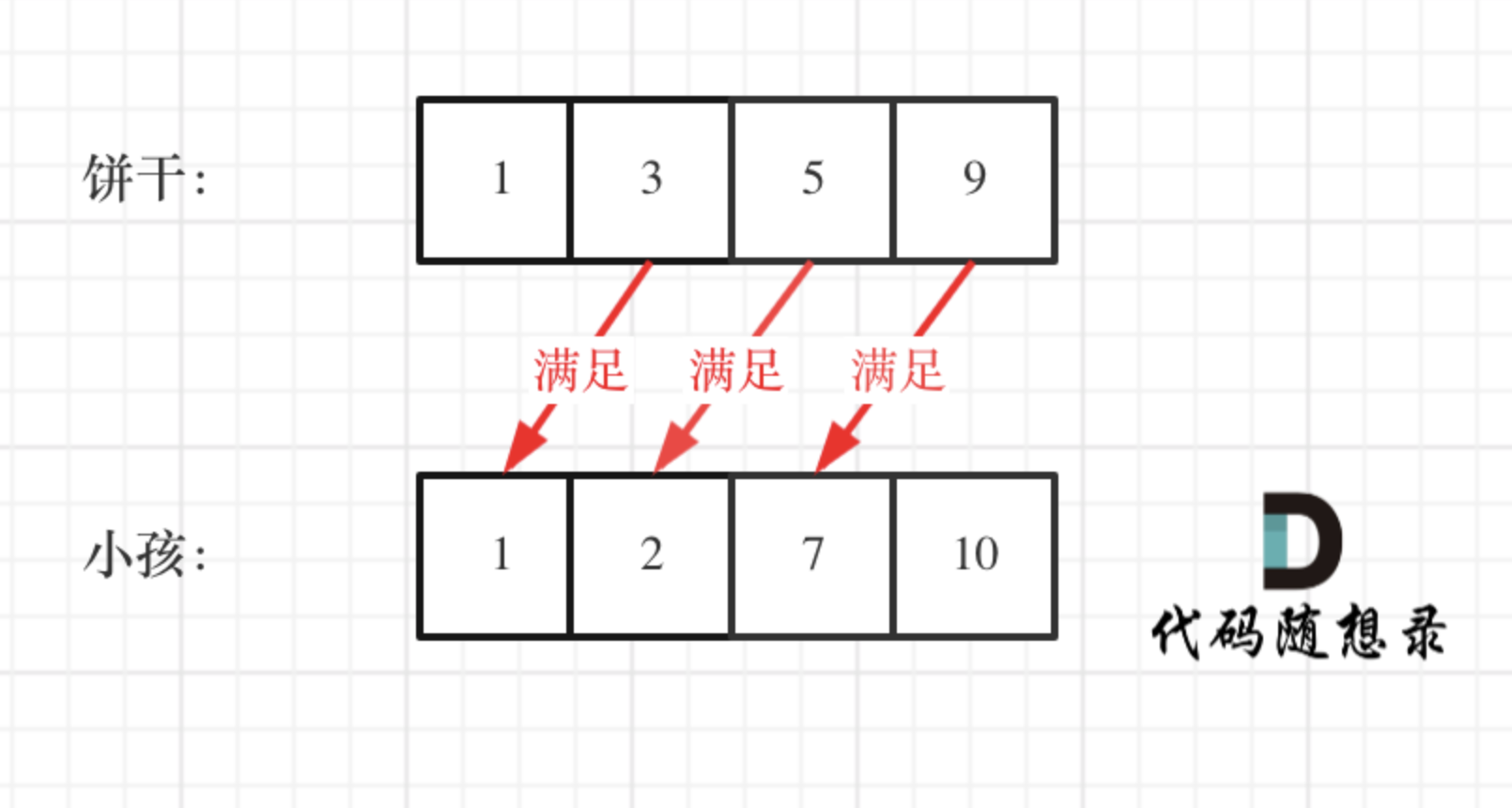
步骤:
1、两个数组进行排序
2、外循环遍历小孩胃口
3、内循环遍历饼干
1 | var findContentChildren = function(g, s) { |

策略:size大的饼干给胃口大的小孩。
步骤:
1、两个数组进行排序
2、外循环遍历小孩胃口
3、内循环遍历饼干
1 | var findContentChildren = function(g, s) { |
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
这么说有点抽象,来举一个例子:
例如,有一堆钞票,你可以拿走十张,如果想达到最大的金额,你要怎么拿?
指定每次拿最大的,最终结果就是拿走最大数额的钱。
每次拿最大的就是局部最优,最后拿走最大数额的钱就是推出全局最优。
再举一个例子如果是 有一堆盒子,你有一个背包体积为n,如何把背包尽可能装满,如果还每次选最大的盒子,就不行了。这时候就需要动态规划。动态规划的问题在下一个系列会详细讲解。
很多同学做贪心的题目的时候,想不出来是贪心,想知道有没有什么套路可以一看就看出来是贪心。
说实话贪心算法并没有固定的套路。
所以唯一的难点就是如何通过局部最优,推出整体最优。
那么如何能看出局部最优是否能推出整体最优呢?有没有什么固定策略或者套路呢?
不好意思,也没有! 靠自己手动模拟,如果模拟可行,就可以试一试贪心策略,如果不可行,可能需要动态规划。
有同学问了如何验证可不可以用贪心算法呢?
最好用的策略就是举反例,如果想不到反例,那么就试一试贪心吧。
可有有同学认为手动模拟,举例子得出的结论不靠谱,想要严格的数学证明。
一般数学证明有如下两种方法:
数学归纳法
反证法
看教课书上讲解贪心可以是一堆公式,估计大家连看都不想看,所以数学证明就不在我要讲解的范围内了,大家感兴趣可以自行查找资料。
面试中基本不会让面试者现场证明贪心的合理性,代码写出来跑过测试用例即可,或者自己能自圆其说理由就行了。
举一个不太恰当的例子:我要用一下1+1 = 2,但我要先证明1+1 为什么等于2。严谨是严谨了,但没必要。
虽然这个例子很极端,但可以表达这么个意思:刷题或者面试的时候,手动模拟一下感觉可以局部最优推出整体最优,而且想不到反例,那么就试一试贪心。
例如刚刚举的拿钞票的例子,就是模拟一下每次拿做大的,最后就能拿到最多的钱,这还要数学证明的话,其实就不在算法面试的范围内了,可以看看专业的数学书籍!
所以这也是为什么很多同学通过(accept)了贪心的题目,但都不知道自己用了贪心算法,因为贪心有时候就是常识性的推导,所以会认为本应该就这么做!
那么刷题的时候什么时候真的需要数学推导呢?
例如这道题目:链表:环找到了,那入口呢? (opens new window),这道题不用数学推导一下,就找不出环的起始位置,想试一下就不知道怎么试,这种题目确实需要数学简单推导一下。
想到局部最优是什么,然后想不出来反例,就可以用贪心算法了。
看了卡哥视频,就是要多刷题,见过套路才会写,没见过套路的一些比较难的题目很难通过总结规律做出来,因为每道题的规律都不同。
https://leetcode.cn/problems/maximize-sum-of-array-after-k-negations/description/

1 | var largestSumAfterKNegations = function(nums, k) { |
四数之和和三数之和的思路是一脉相承的,只不过三数之和是一层for循环,每次遍历一个数。四数之和可以用双层for循环。
剪枝的思路与三数之和有些不同呢,三数之和的目标值是0,而四数之和的目标值是不固定的,如果遇到负数情况会有所不同。num>target不能直接退出,如果后面加负数的话,target会变小。
1 | var fourSum = function(nums, target) { |

1、拿这个nums数组来举例,首先将数组排序,然后有一层for循环,i从下标0的地方开始,同时定一个下标left 定义在i+1的位置上,定义下标right 在数组结尾的位置上。
2、依然还是在数组中找到 abc 使得a + b +c =0,我们这里相当于 a = nums[i],b = nums[left],c = nums[right]。
3、接下来如何移动left 和right呢, 如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了,因为数组是排序后了,所以right下标就应该向左移动,这样才能让三数之和小一些。
4、如果 nums[i] + nums[left] + nums[right] < 0 说明 此时 三数之和小了,left 就向右移动,才能让三数之和大一些,直到left与right相遇为止。
a去重逻辑
当前遍历元素和前一个元素重复是,跳过
b和c去重逻辑
1 | var threeSum = function(nums) { |
我的初始想法是用回溯算法,但是这个方法在处理较长的数组时会超时。
1 | // 回溯算法 |
本题解题步骤:
1 | var fourSumCount = function(nums1, nums2, nums3, nums4) { |
https://leetcode.cn/problems/remove-nth-node-from-end-of-list/description/
1 | var removeNthFromEnd = function(head, n) { |
首先使用虚拟结点,方便处理实际的头结点逻辑,也就是说包括头结点在内的所有结点,处理逻辑是一致的。
定义快慢指针,fast和slow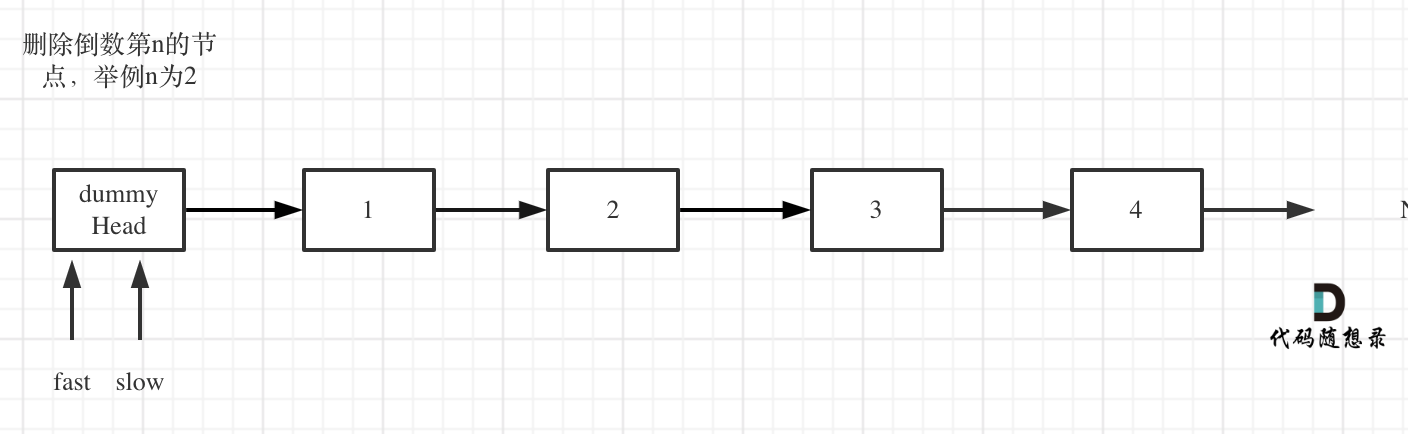
fast比slow先走n+1步,这样当fast走到最后节点的下一个结点null的时候,slow正好指向将被删除结点的上一个结点。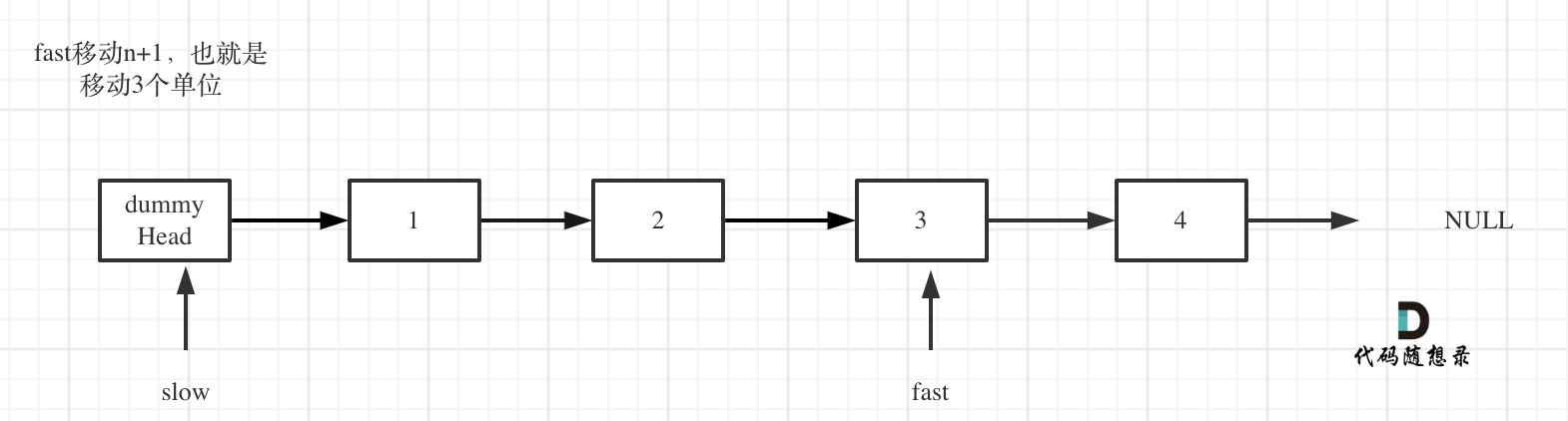
fast和slow同时移动指向末尾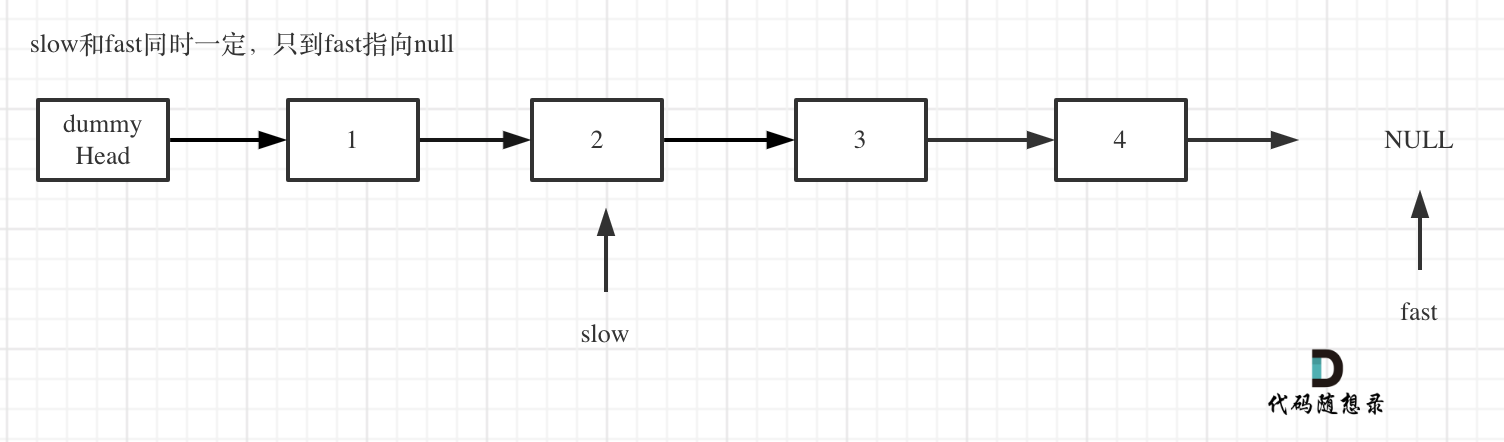
删除slow指向的下一个结点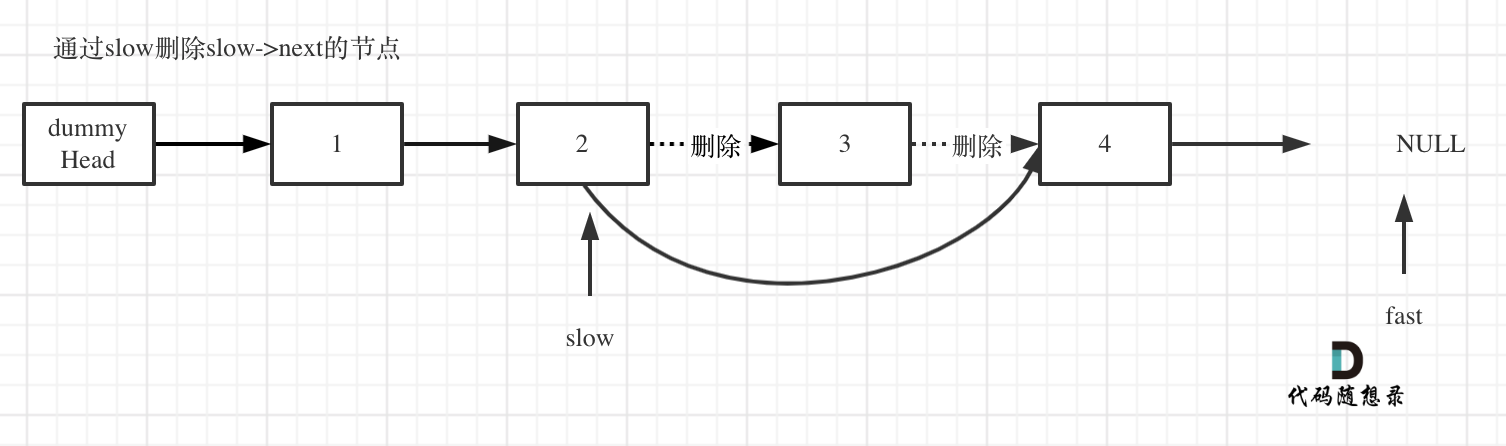
1 | var removeNthFromEnd = function(head, n) { |
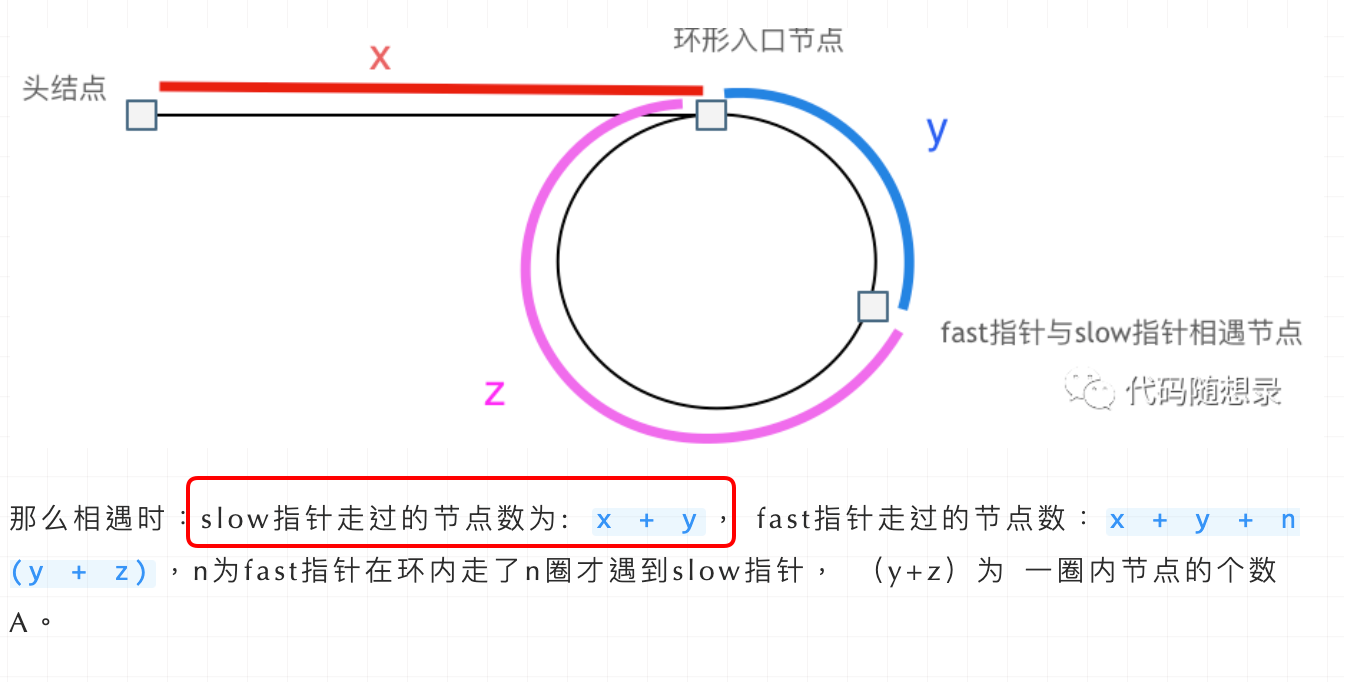
这就意味着,从链表的头部到环的入口的距离等于从快慢指针相遇点到环的入口的距离。所以,当快慢指针相遇后,我们可以将一个指针移动到链表的头部,然后两个指针同时移动,当它们再次相遇时,就是环的入口。
这就是使用快慢指针可以找到环形链表的数学原理。

1 | var detectCycle = function(head) { |
在每一步,pA 和 pB 都会向前移动一步。如果 pA 到达了链表 headA 的末尾,那么将它重置到链表 headB 的头部;同样,如果 pB 到达了链表 headB 的末尾,那么将它重置到链表 headA 的头部。
这样,pA 和 pB 就会同时遍历两个链表。如果两个链表有交点,那么 pA 和 pB 就会在交点处相遇,此时 pA === pB,循环结束,返回 pA(或 pB)即可。如果两个链表没有交点,那么 pA 和 pB 就会同时到达两个链表的末尾,此时 pA === pB === null,循环结束,返回 pA(或 pB,此时为 null)。
这个算法的时间复杂度是 O(N),空间复杂度是 O(1),其中 N 是两个链表的总长度。
假设链表A的长度为a+c,链表B的长度为b+c,其中c是两个链表共享的部分的长度。当我们从链表A的头部和链表B的头部同时开始遍历,到达各自链表末尾时,我们已经遍历了a+c和b+c个节点。此时,如果我们将指针切换到另一个链表的头部继续遍历,那么当两个指针相遇时,它们都已经遍历了a+b+c个节点。
因此,无论两个链表的长度如何,当两个指针相遇时,它们都已经遍历了相同数量的节点。如果两个链表有交点,那么这个交点就是两个指针的相遇点;如果两个链表没有交点,那么两个指针就会在遍历了a+b+c个节点后同时到达链表的末尾,此时pA和pB都为null,循环结束。
这就是为什么这个规律可以找出两个链表的交点,或者确定两个链表没有交点的原因
1 | var getIntersectionNode = function(headA, headB) { |
首先确定两个链表的长度
对齐:这个过程用图片示意如下;较短的那个位置是关键。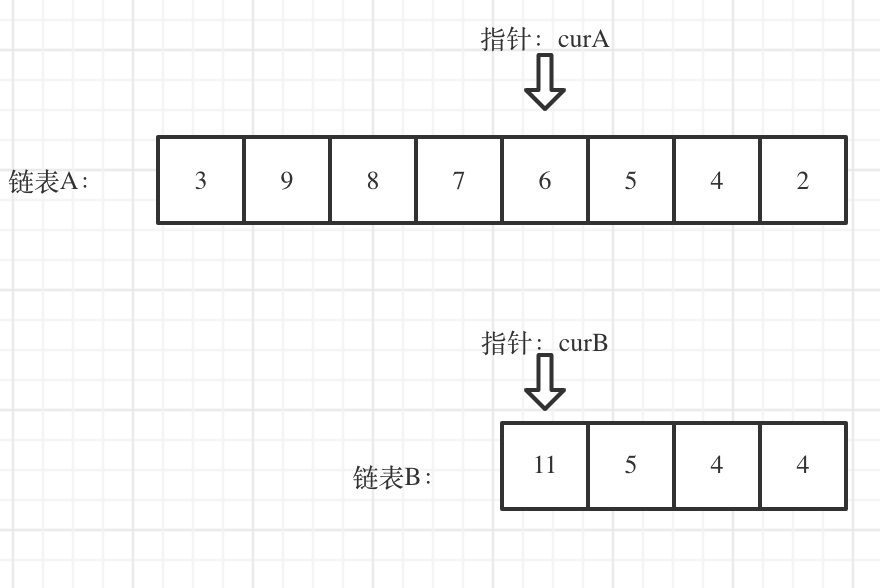
找到相同的结点返回即可
1 | var getIntersectionNode = function(headA, headB) { |
https://leetcode.cn/problems/swap-nodes-in-pairs/description/
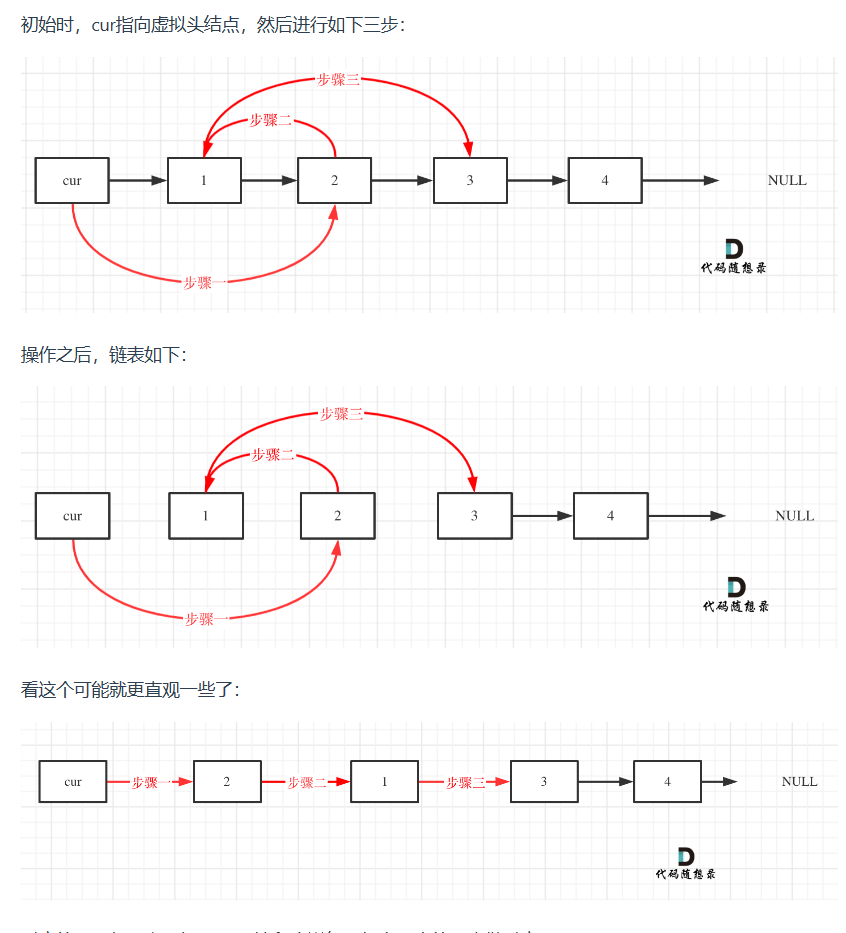
1 | var swapPairs = function(head) { |