回溯算法

发表于2024-04-01更新于2024-04-14

回溯算法

回溯算法基本理论

是什么：

回溯采用是错得方法解决问题，一旦发现当前步骤失败，回溯算法就会返回上一个步骤

解决哪些问题：

  • 组合问题（组合不强调顺序，而排列强调）
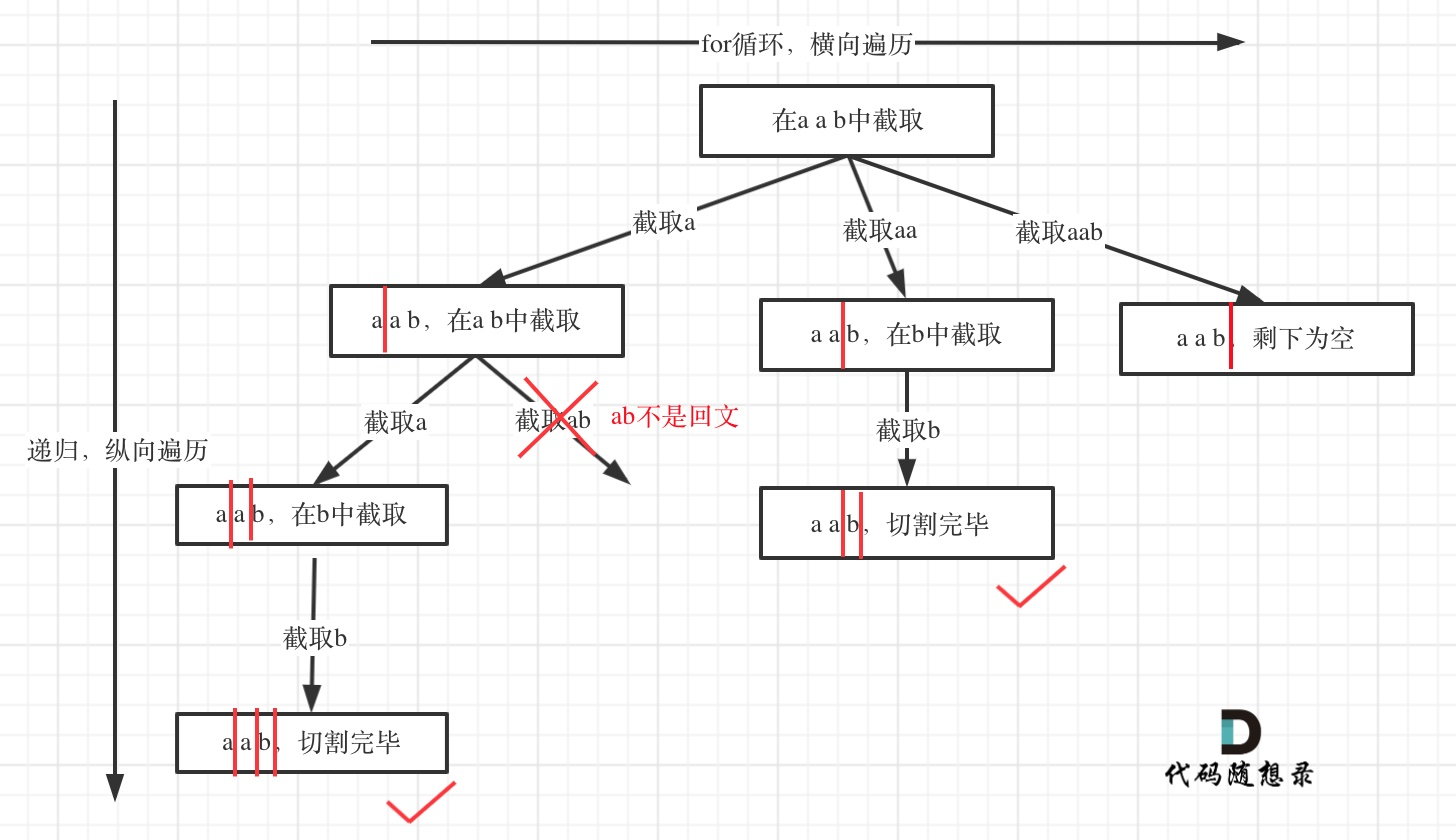
  • 切割问题
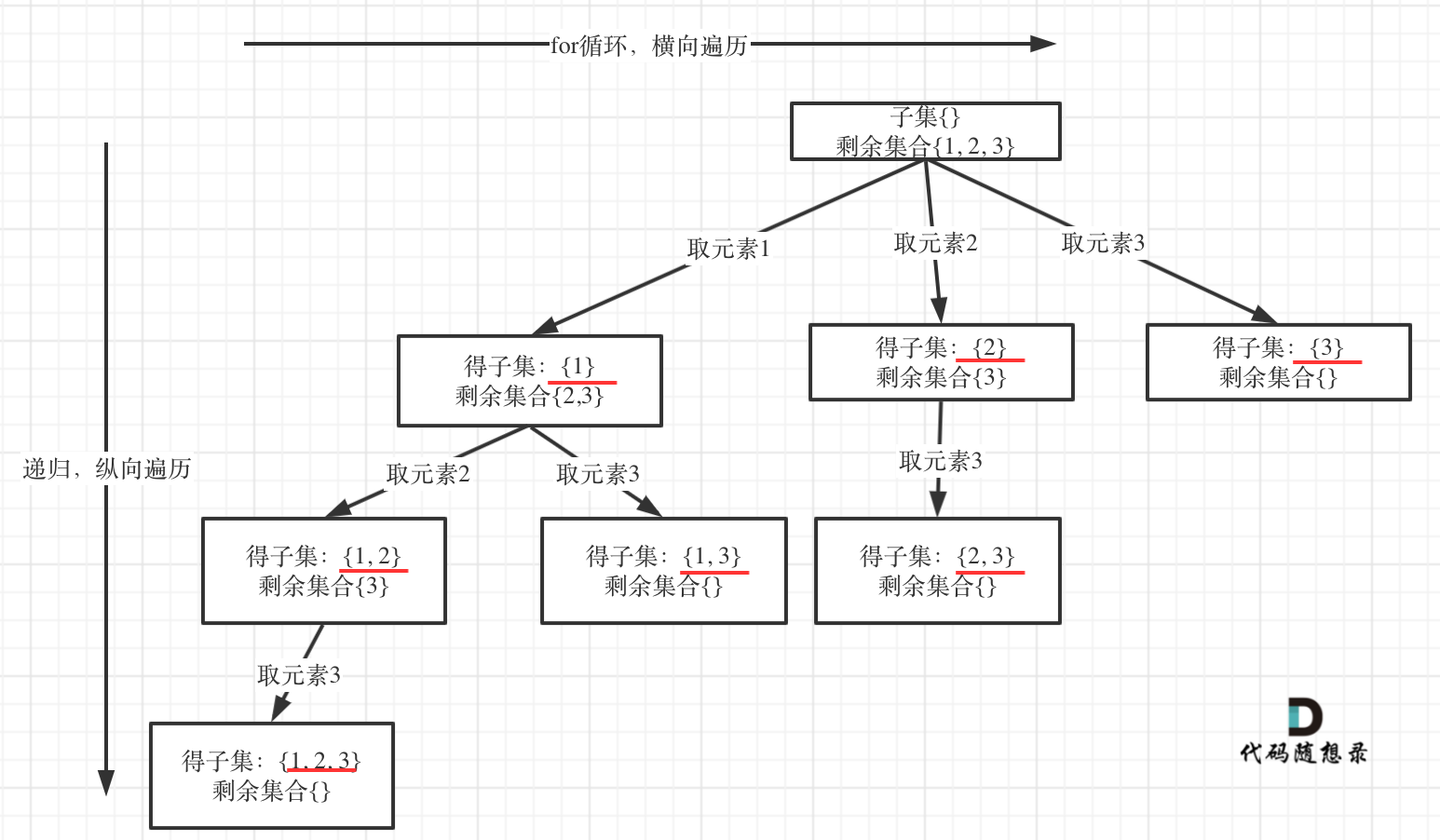
  • 子集问题
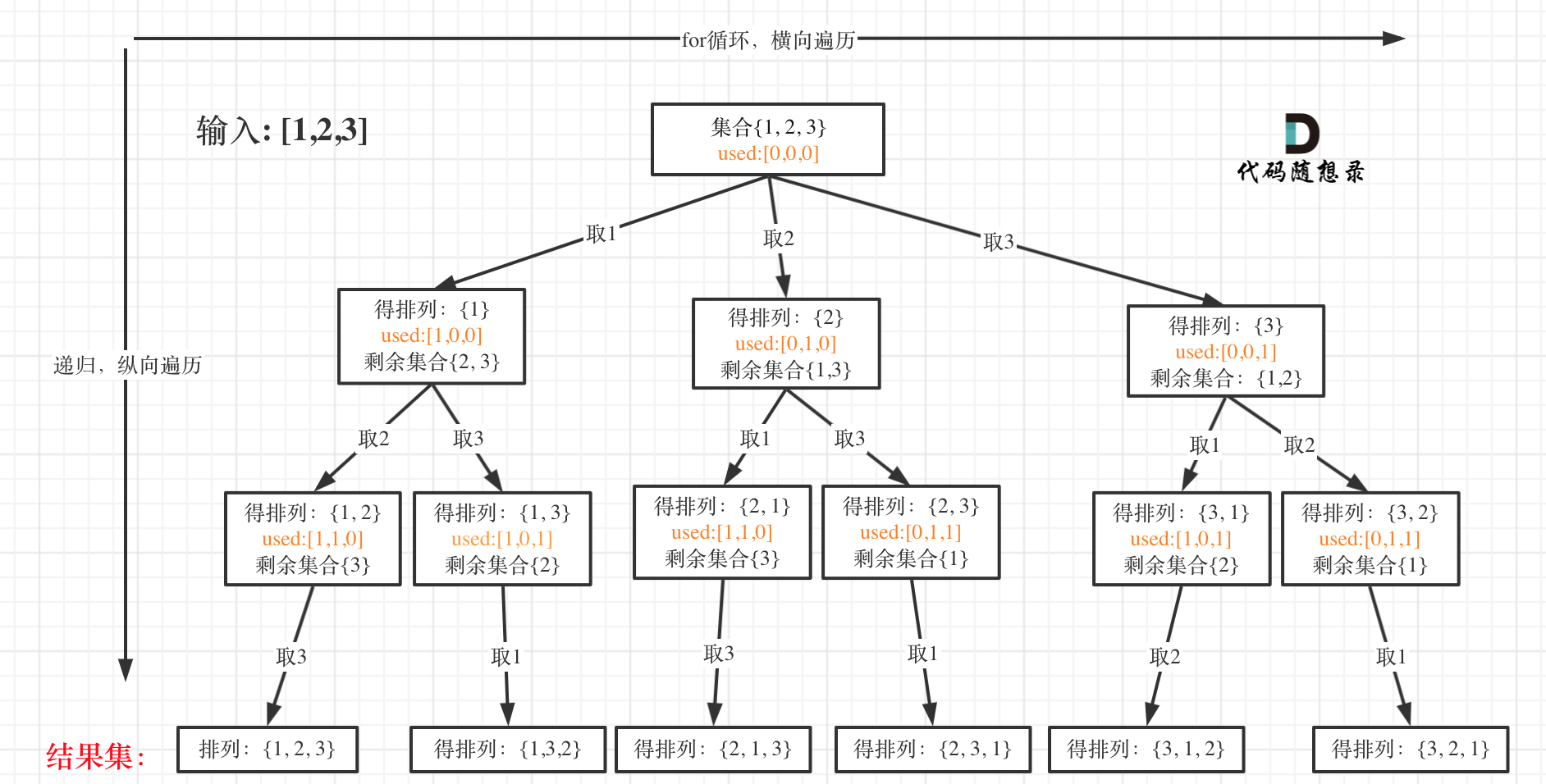
  • 排列问题
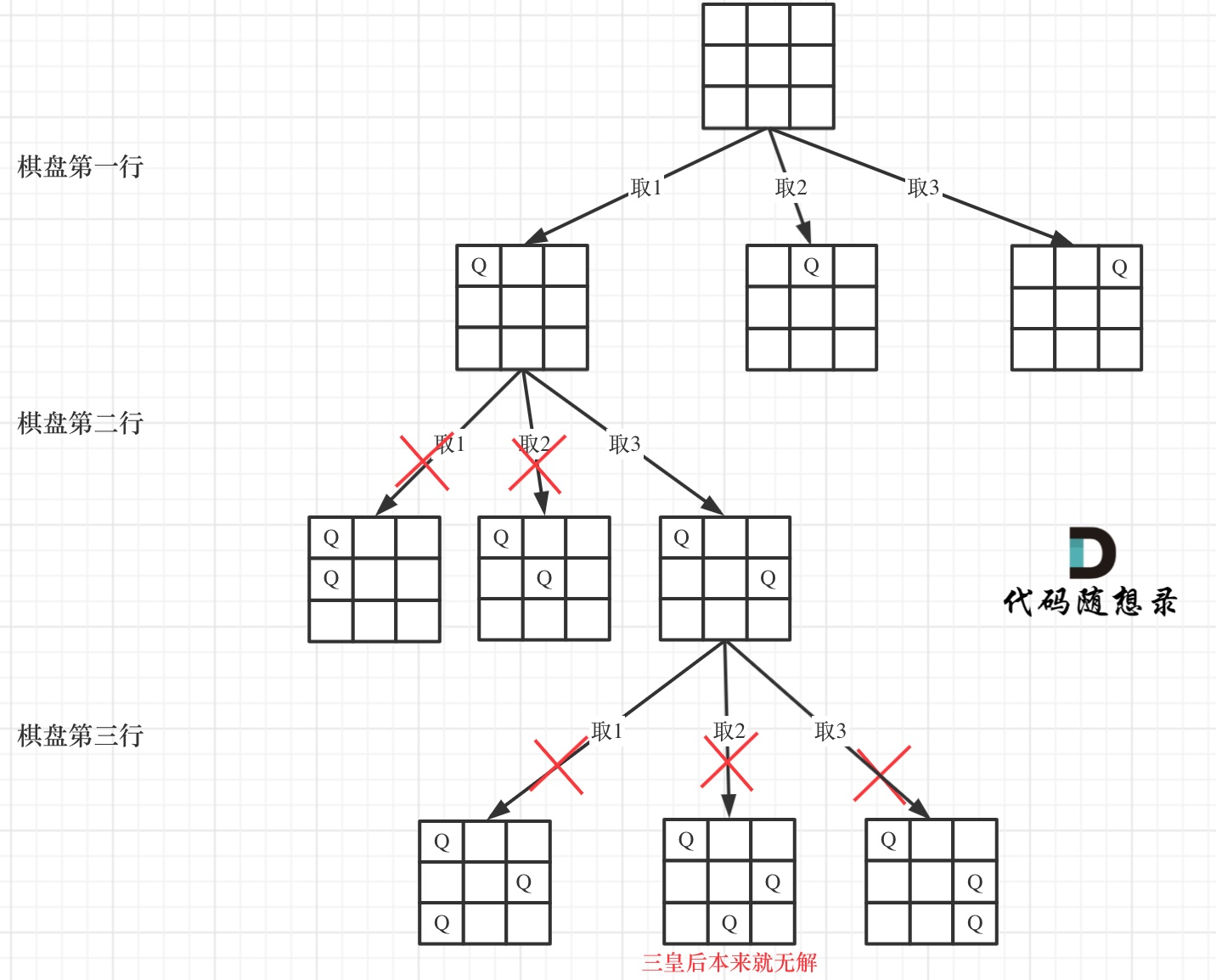
  • 棋盘问题

如何理解回溯法

回溯法都可以抽象为一个树形结构。一个n叉树

图 0

回溯法的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 递归函数没有返回值
void backtrading(参数){
  // 递归终止条件
  if (终止条件){ //通常在叶子节点
    //收集结果
    return
  }
  // 单层搜索
  for (集合得元素集){ //遍历集合中的每一个元素
    // 处理节点
    // 递归函数
    // 回溯
  }
  return
}

回溯算法剪枝

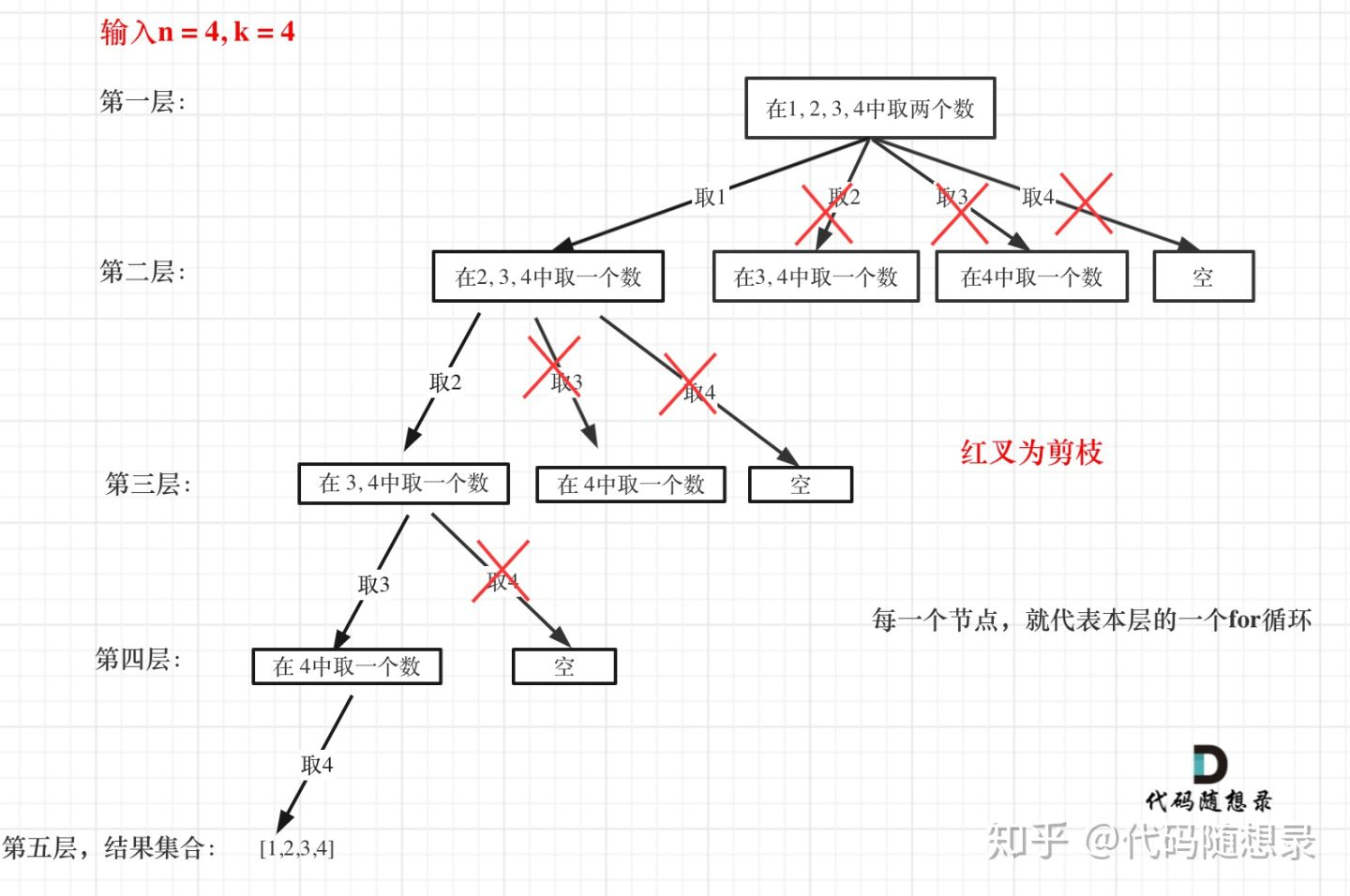
剪枝一般都是在for循环的i的范围上做文章，例如下面的组合题目，确定i至多从哪里开始。
图 4

回溯算法题目

组合问题

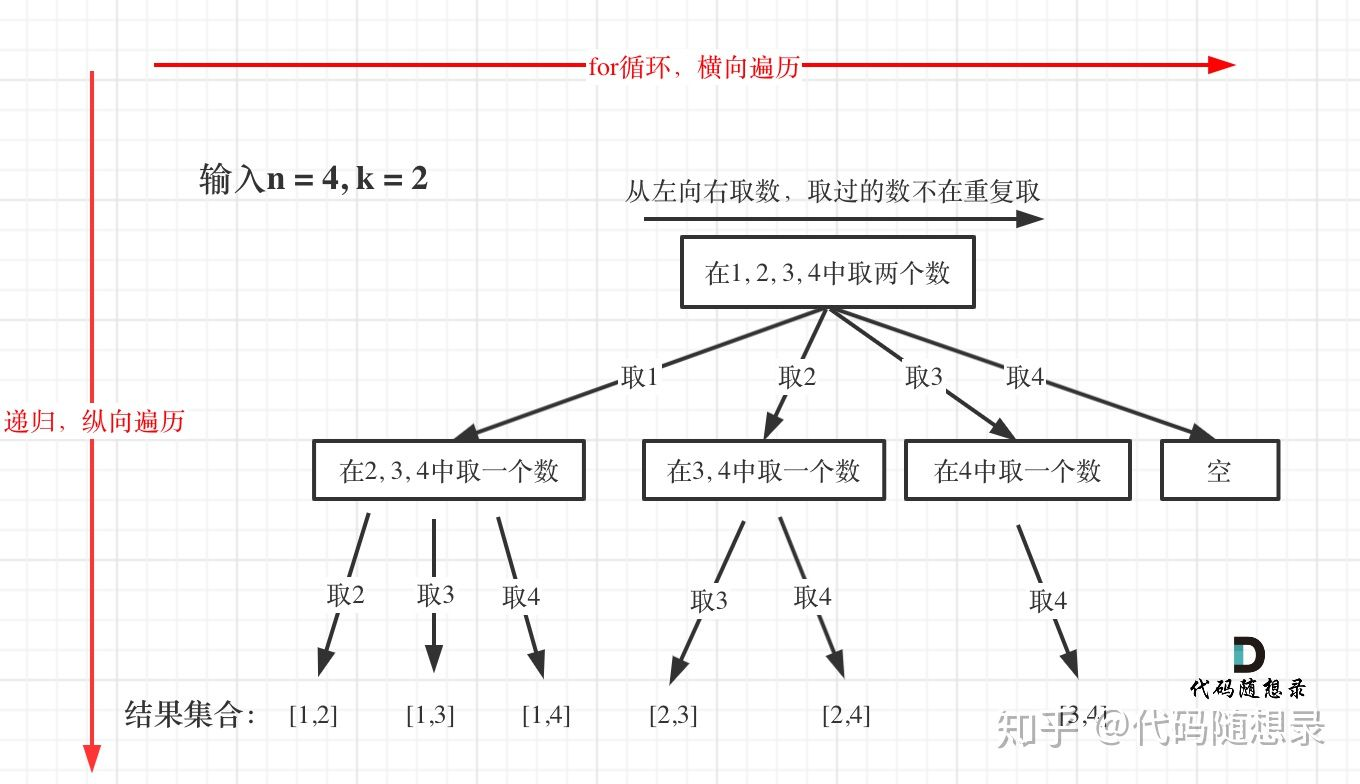
题目：https://leetcode.cn/problems/combinations/description/

图 2

未剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var combine = function(n, k) {
  var path = [];  // 用来存放每一个结果
  var res = [];  //存放所有结果的数组
  //确定参数
  const backTrading = (n, k, startIndex) => { //startIndex搜索的起始位置
    //终止条件
    if(path.length === k){
      //注意这里要深拷贝一下path，因为path是引用类型，后续的操作会改变path的值
      res.push([...path]); //将path的值push到res中
      return;
    }
    // 单层递归逻辑
    for(let i = startIndex; i <= n; i++){
      path.push(i);
      backTrading(n, k, i + 1); //递归,起始位置+1
      path.pop(); //回溯的过程，弹出最后一个元素
    }
  }
  backTrading(n, k, 1); //调用backTrading函数,第一次竟然忘了这一步
  return res;
};

剪枝

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// path.length 已选取的元素的大小
// k-path.length 还需要的元素
// n-(k-path.length)+1 i的至多从该位置开始取
var combine = function(n, k) {
  var path = [];  // 用来存放每一个结果
  var res = [];  //存放所有结果的数组
  //确定参数
  const backTrading = (n, k, startIndex) => { //startIndex搜索的起始位置
    //终止条件
    if(path.length === k){
      //注意这里要深拷贝一下path，因为path是引用类型，后续的操作会改变path的值
      res.push([...path]); //将path的值push到res中
      return;
    }
    // 单层递归逻辑
    //剪枝在for循环停止的位置做文章
    for(let i = startIndex; i <= (n-(k-path.length)+1); i++){
      path.push(i);
      backTrading(n, k, i + 1); //递归,起始位置+1
      path.pop(); //回溯的过程，弹出最后一个元素
    }
  }
  backTrading(n, k, 1); //调用backTrading函数,第一次竟然忘了这一步
  return res;
};

组合总和 III

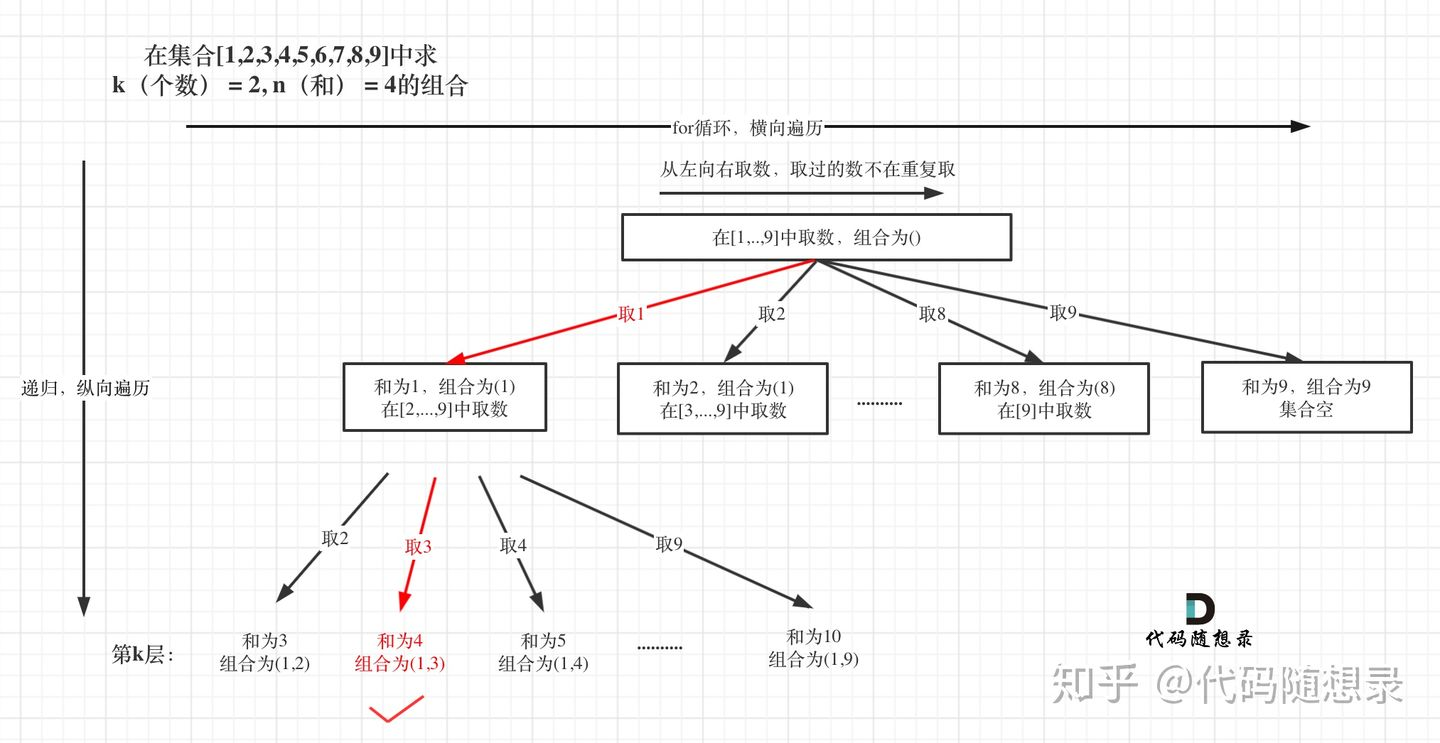
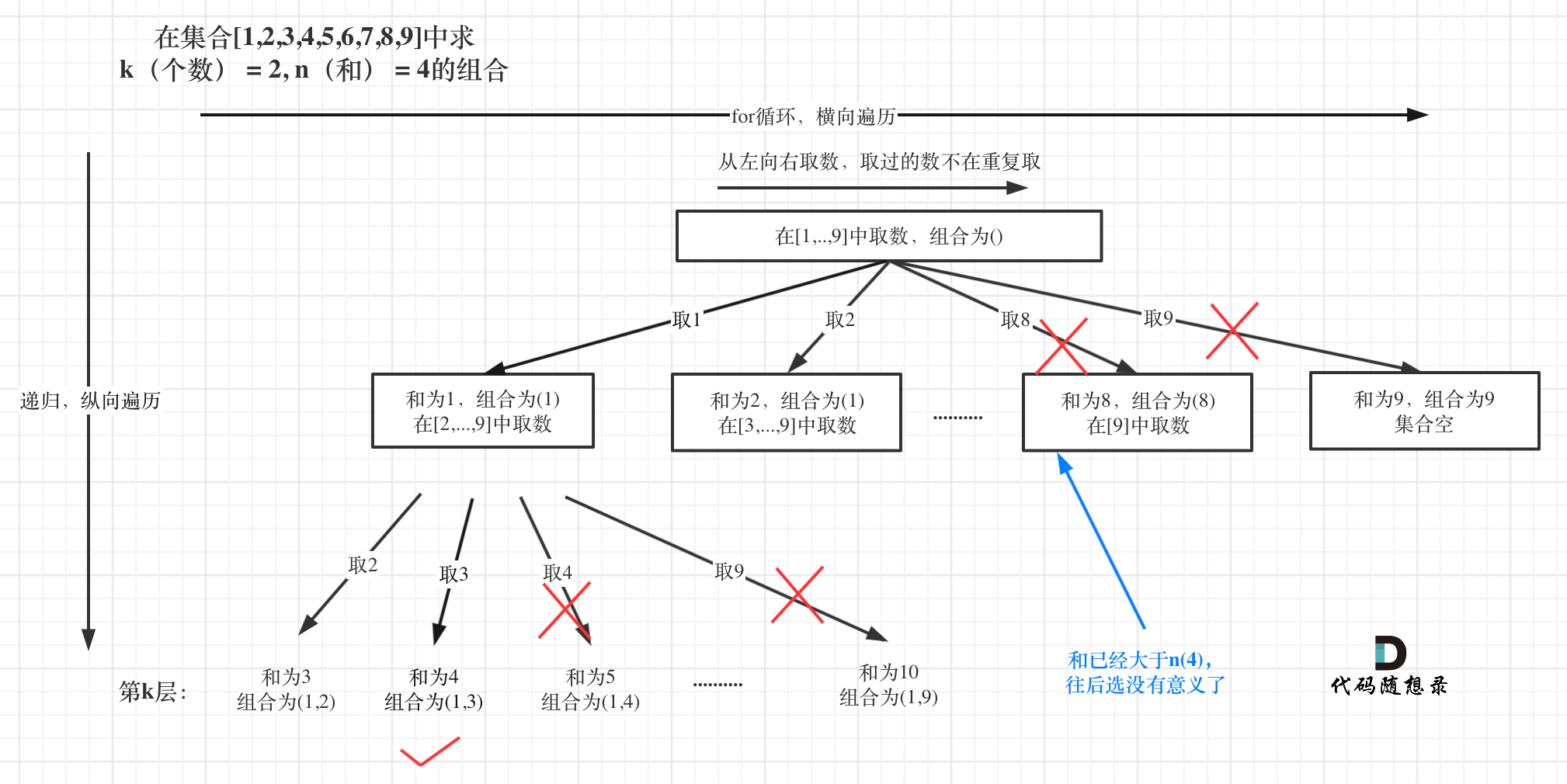
https://leetcode.cn/problems/combination-sum-iii/description/

图 5

图 6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//加了剪枝操作
var combinationSum3 = function(k, n) {
  let path = []   //一维数组，用来存放符合条件的组合
  let res = []    //二维数组，用来存放符合条件的组合数组
  const backTrading = (n,k,sum,startIndex)=>{ //sum是当前path数组的和
    if(sum>n) return  //这是一个剪枝操作
    if(path.length ===k){
      if(sum === n){
        res.push([...path])
      }
      return
    }
  // i的边界的控制也是剪枝操作
  for(let i = startIndex;i<=(9-(k-path.length)+1);i++){
    sum += i
    path.push(i)
    backTrading(n,k,sum,i+1) //这里是深入分支
    sum -= i    //回溯，这里是广度的遍历，挨个遍历每一个元素
    path.pop()
  }
}
  backTrading(n,k,0,1)
  return res
};

电话号码的字母组合

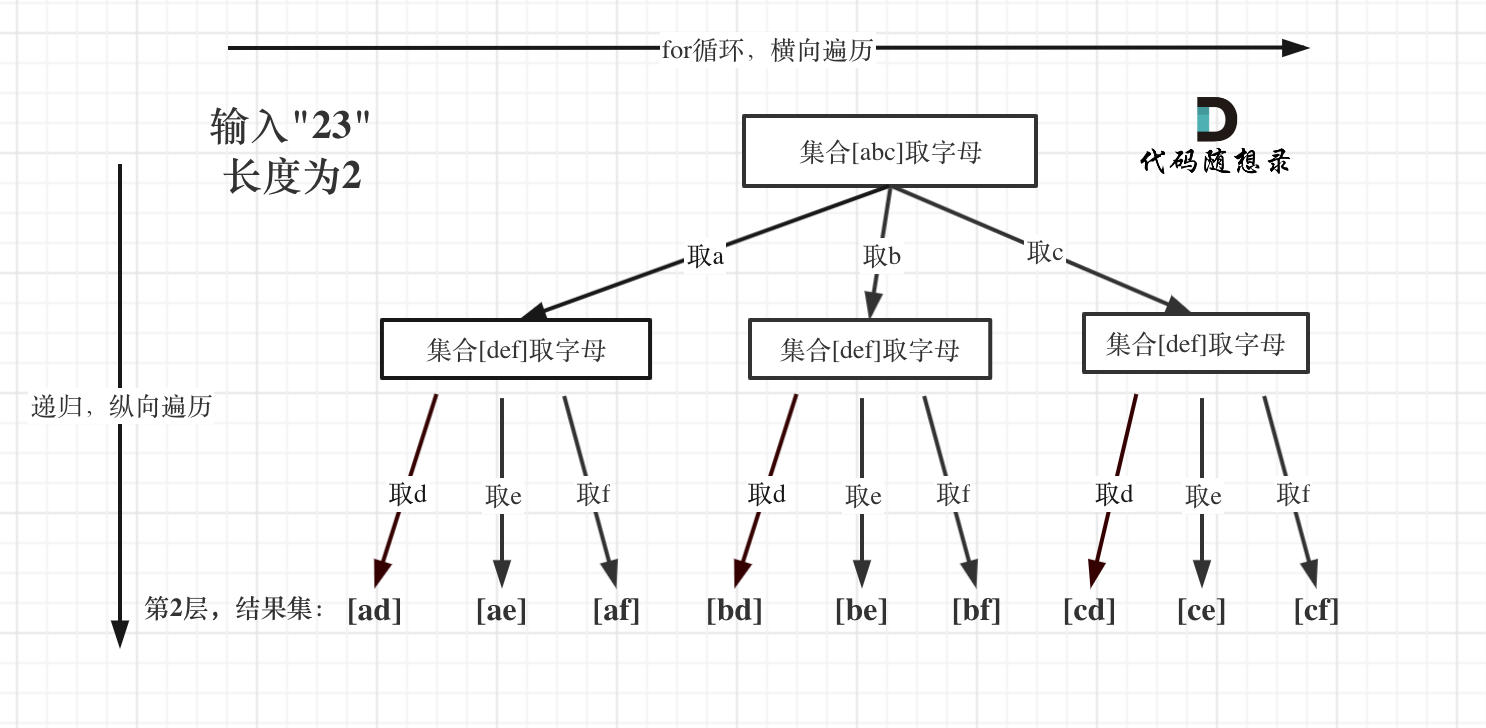
https://leetcode.cn/problems/letter-combinations-of-a-phone-number/description/

解题思路

  • 先做数字和字母的映射
  • 通过树形结构梳理思路

图 7

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
var letterCombinations = function(digits) {
  //先做一个映射表
  const map = new Map()
  map.set('2','abc')
  map.set('3','def')
  map.set('4','ghi')
  map.set('5','jkl')
  map.set('6','mno')
  map.set('7','pqrs')
  map.set('8','tuv')
  map.set('9','wxyz')
  let str = ''   //收获单个结果
  let res = []
  const backTrading = (digits,index)=>{
    if(!digits) return
    if(index === digits.length){  //终止条件
      res.push(str)
      return
    }
    //单层逻辑
    let digit = digits[index]  //找到数字
    let letters = map.get(digit)   // 根据数字在映射表中找到对应的字母
    for(let i=0;i<letters.length;i++){
      str += letters[i]
      backTrading(digits,index+1)
      str = str.slice(0,str.length-1) //回溯
    }
  }
  backTrading(digits,0)
  return res
};

组合总和

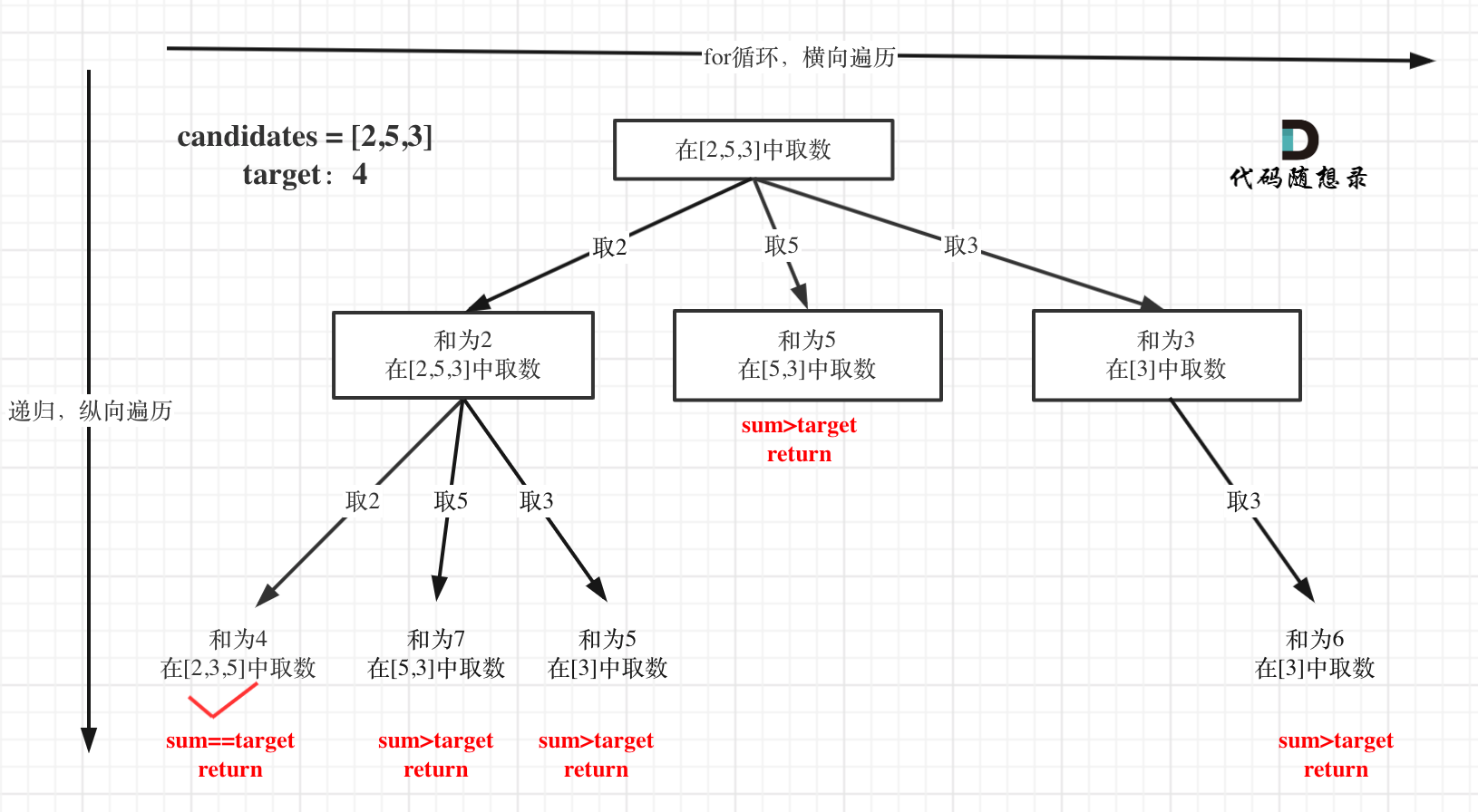
https://leetcode.cn/problems/combination-sum/description/

数组中没有0且没有重复数字。

图 8

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var combinationSum = function(candidates, target) {
  //递归终止条件
  let path = []
  let res = []
  const backTraking = (candidates,target,sum,startIndex)=>{
    if (sum > target) return
    if (sum === target) {
      res.push(path.slice())  //深拷贝
      return
    }
    for(let i = startIndex;i<candidates.length;i++){
      path.push(candidates[i])
      sum += candidates[i]
      backTraking(candidates,target,sum,i) //可以重复i不加1喽
      sum -= candidates[i]
      path.pop()
    }
  }
  backTraking(candidates,target,0,0)
  return res
};

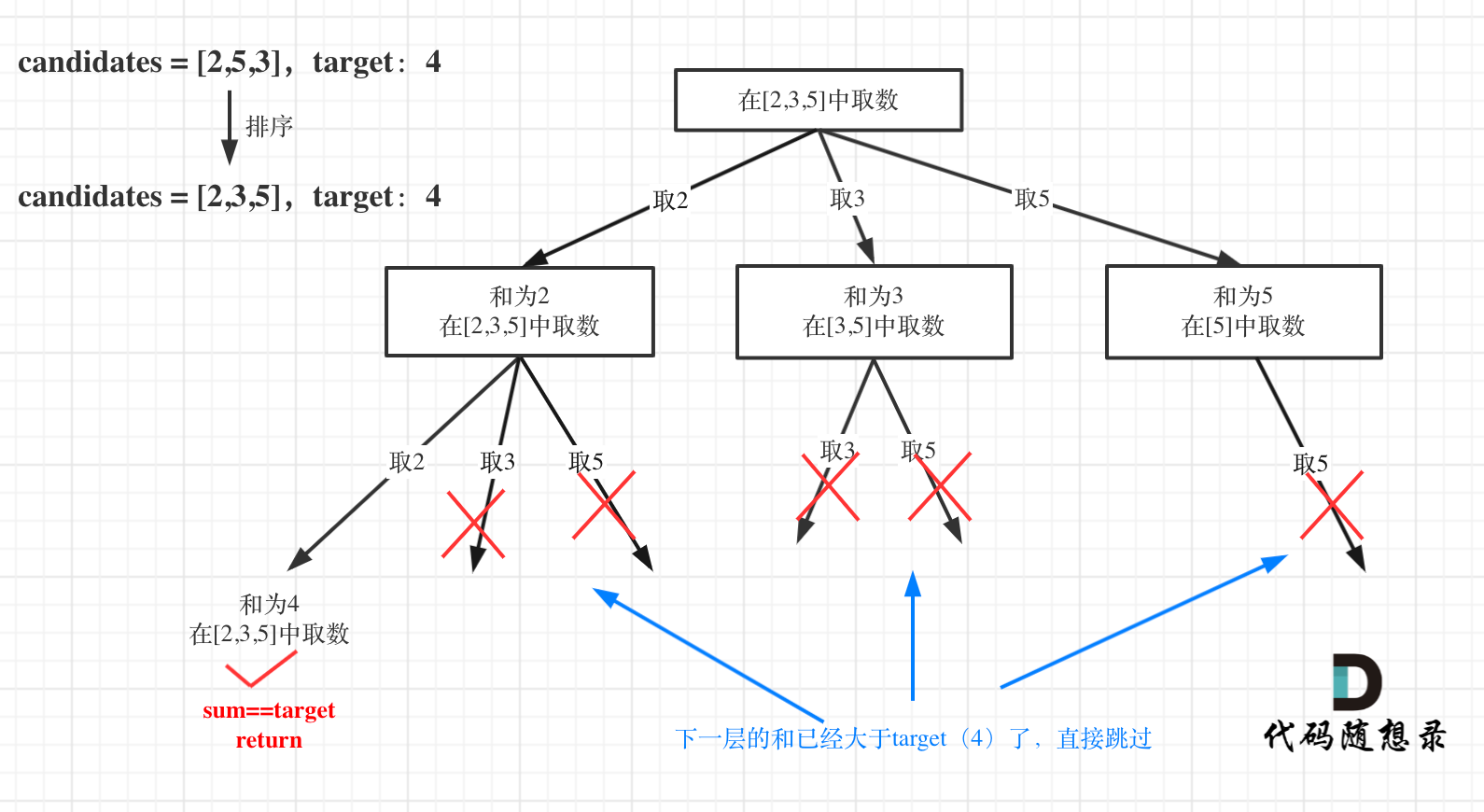
剪枝
图 9

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
var combinationSum = function(candidates, target) {
  //递归终止条件
  let path = []
  let res = []
  const backTraking = (candidates,target,sum,startIndex)=>{
    // if (sum > target) return
    if (sum === target) {
      res.push(path.slice())  //深拷贝
      return
    }
    for(let i = startIndex;i<candidates.length;i++){
      if (candidates[i] + sum > target) continue; //剪枝
      path.push(candidates[i])
      sum += candidates[i]
      backTraking(candidates,target,sum,i) //可以重复i不加1喽
      sum -= candidates[i]
      path.pop()
    }
  }
  backTraking(candidates,target,0,0)
  return res
};

组合总和 II

https://leetcode.cn/problems/combination-sum-ii/description/

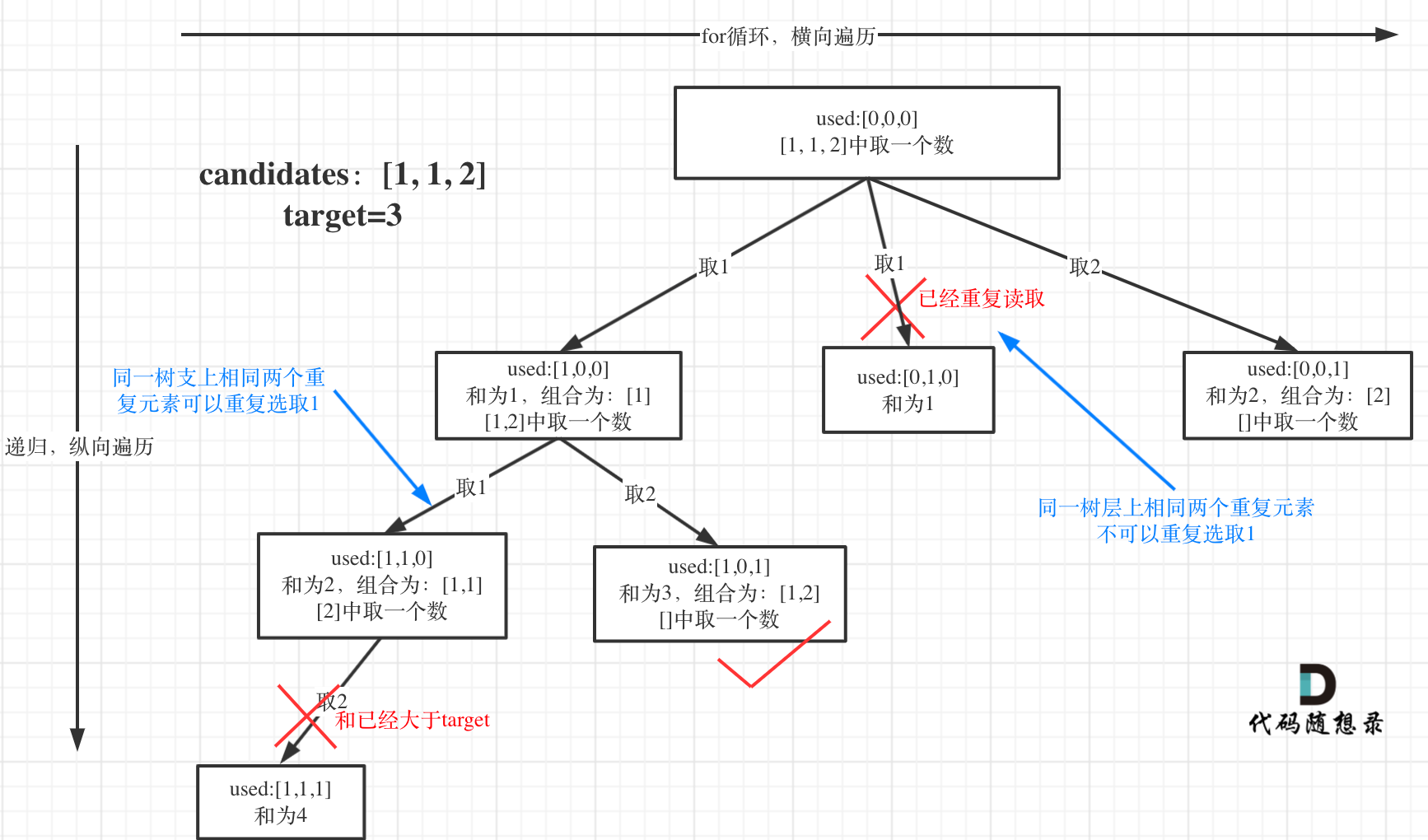
难点在于：结果中不能有重复的结果[1,7],[7,1]。但是能原数组中有两个1，有可以有[1,1,6]。

图 10

树层去重和树枝去重

https://www.programmercarl.com/0040.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8CII.html#%E6%80%9D%E8%B7%AF

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var combinationSum2 = function(candidates, target) {
  let path = []
  let res = []
  // 进行排序
  candidates.sort((a,b)=>a-b)
  const backTracking = (candidates,target,sum,startIndex,used)=>{
    if (sum === target){
      res.push(path.slice())
      return
    }
    for(let i = startIndex;i<candidates.length;i++){
      if (sum + candidates[i] > target) continue  //剪枝
      // i>0是为了保证i-1有意义
      // used[i-1]=false，说明此时处于树层的状态，即同一树层上的前一个元素已经被撤销，所以此时可以继续使用
      if (i > 0 && candidates[i] === candidates[i-1] && !used[i-1]) continue  //数层去重的而过程，前提是数组有序
      path.push(candidates[i])
      sum += candidates[i]
      used[i] = true  //标记使用过
      backTracking(candidates,target,sum,i+1,used)
      //回溯
      sum -= candidates[i]
      path.pop()
      used[i] = false
    }
  }
  backTracking(candidates,target,0,0,new Array(candidates.length).fill(false))
  return res
};

分割回文子串

https://leetcode.cn/problems/palindrome-partitioning/description/

图 11

难点：

  • 切割问题和组合是一样的，之前选择的元素下标，相当于这里的切割线
  • 如何表示切割的字串[startIndex,i]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
var partition = function(s) {
  let path = [] //一维数组，用来存放每一次的结果
  let res = [] //二维数组，用来存放所有的结果、
  const backTraking = (s,startIndex)=>{
    if(startIndex >= s.length){  //到了叶子就节点了，将结果放入res中
      res.push(path.slice())
      return
    }
    // 单层搜索逻辑
    for(let i=startIndex;i<s.length;i++){
      // 如果是回文子串，才添加到path中，否则直接continue
      if(isPlalindrome(s,startIndex,i)){
        path.push(s.substring(startIndex,i+1))
        backTraking(s,i+1)
        path.pop()
      }
    }
  }
  const isPlalindrome = (s,left,right)=>{
    //判断是否是回文串的函数
    while(left<right){
      if(s[left] !== s[right]) return false
      left++
      right--
    }
    return true
  }
  backTraking(s,0)
  return res
};

复原IP地址

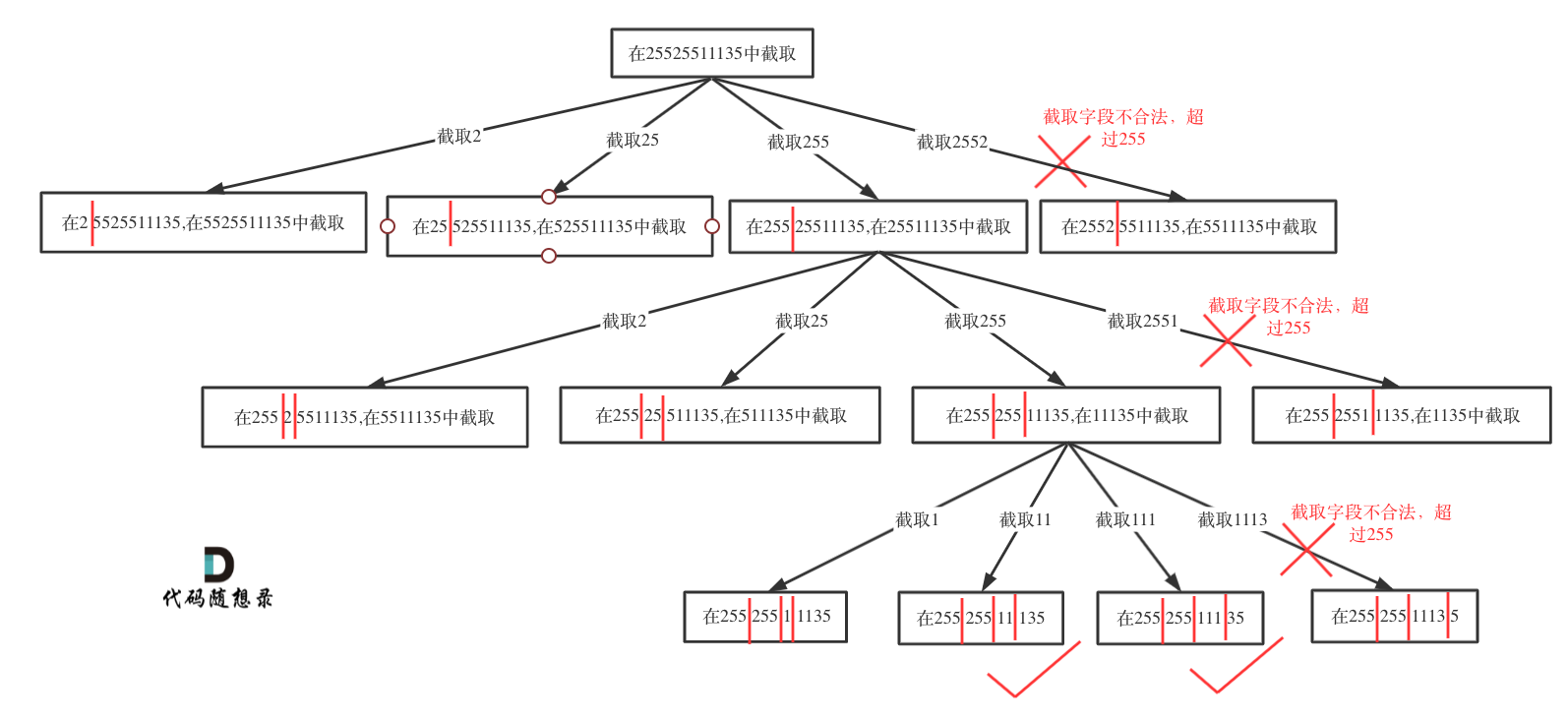
https://leetcode.cn/problems/restore-ip-addresses/description/

合法的IP地址：有效的 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

图 12

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var restoreIpAddresses = function(s) {
  let path = []
  let res = []
  const backTracking = (s,startIndex)=>{
    if(path.length === 4 && startIndex === s.length){
      res.push(path.join('.'))
      return
    }
    //剪枝了，如果path的长度已经是4了，但是startIndex还没有到s的长度，那么就不用再继续了
    if(path.length === 4 && startIndex < s.length) return
    // 剪枝了，如果path的长度不是4了，但是startIndex已经到s的长度了，那么也不用再继续了
    for(let i= startIndex;i<s.length && i<= startIndex+3;i++){
      if (isValid(s,startIndex,i)){
        path.push(s.substring(startIndex,i+1))
        backTracking(s,i+1)
        path.pop()
      }
    }
  }
  const isValid = (s,startIndex,i)=>{
    if(s[startIndex] === '0' && i !== startIndex) return false
    if(parseInt(s.substring(startIndex,i+1)) > 255) return false
    return true
  }
  backTracking(s,0)
  return res
};
前面的一系列都是在叶子节点收获结果，终止条件的写法基本一致
后面开始要从每一个节点收获结果，终止条件的写法发生变化。

子集

https://leetcode.cn/problems/subsets/description/

图 13

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var subsets = function(nums) {
  let path = []
  let res = []
  const backTraking = (nums,startIndex)=>{
    // 每个节点都收获一次、如果终止条件改为>，这一句要放在if的下面，单层搜索逻辑的上面。
    res.push([...path])
    //终止条件是，到了叶子节点
    if(startIndex >= nums.length){
      return //剩余元素为空时，也就是startIndex到达了nums的长度
    }

    for(let i=startIndex;i<nums.length;i++){
      path.push(nums[i])
      backTraking(nums,i+1)
      path.pop()
    }
  }
  backTraking(nums,0)
  return res
};

子集II

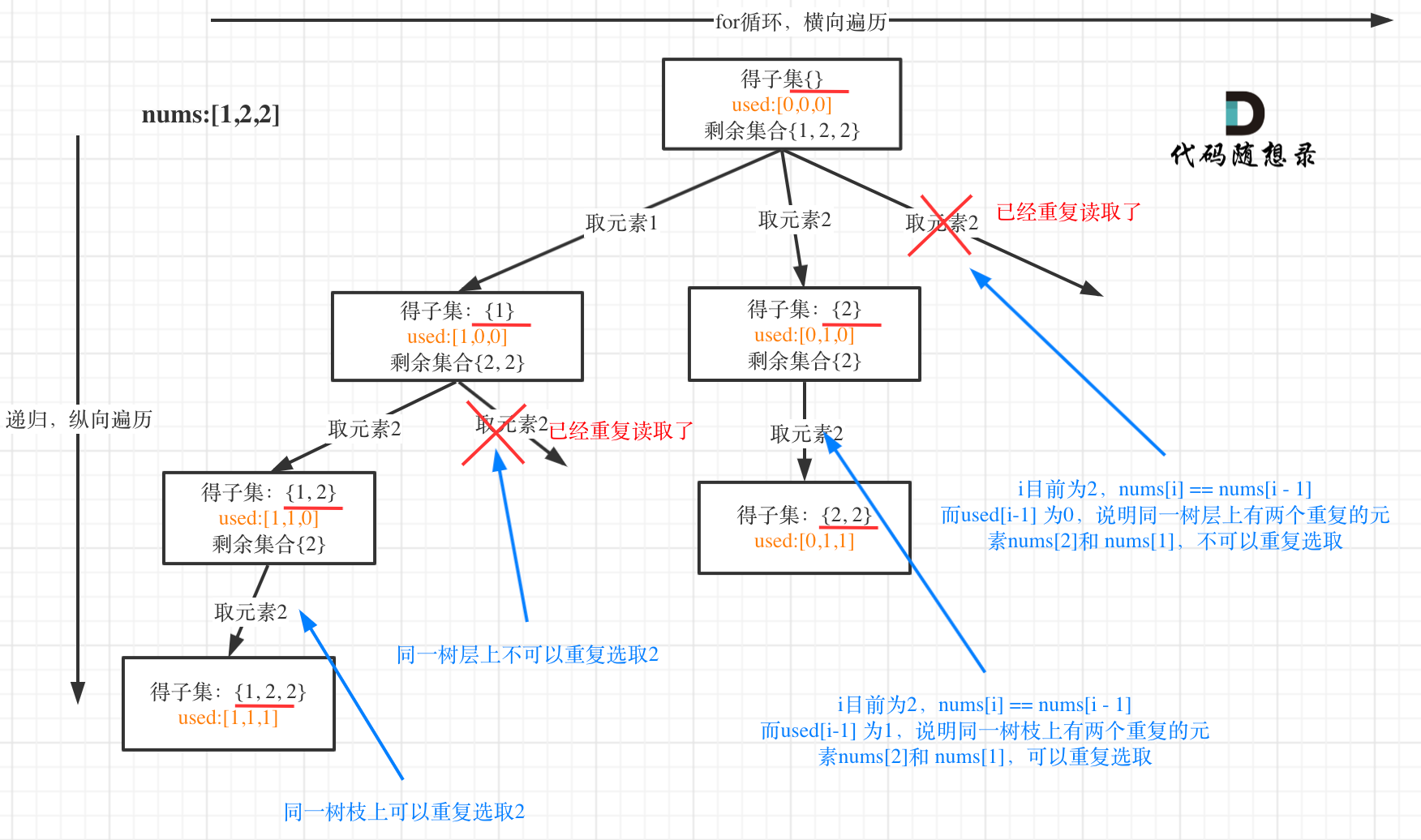
树层去重：确定当前在树层used[i-1]===fasle,当前元素与前一元素相等，i>0

https://leetcode.cn/problems/subsets-ii/description/

图 14

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var subsetsWithDup = function(nums) {
  let path = []
  let res = []
  used = new Array(nums.length).fill(false)
  // 排序
  nums.sort((a, b) => a - b)
  const backTraking = (nums, startIndex, used) => {
    res.push([...path])
    if (startIndex >= nums.length) {
      return
    }
    for (let i = startIndex; i < nums.length; i++) {
      // i>0是为了保证i-1有意义
      // used[i-1]=false，说明此时处于树层的状态，即同一树层上的前一个元素
      // 已经被撤销，所以此时可以继续使用
      if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {
        continue
      }
      path.push(nums[i])
      used[i] = true
      backTraking(nums, i + 1, used)
      path.pop()
      used[i] = false
    }
  }
  backTraking(nums, 0, used)
  return res
};

递增子序列

https://leetcode.cn/problems/non-decreasing-subsequences/

去重方法：由于不能排序，所以这里的树层去重和之前有所差别
之前的题目基本使用used来记录事都使用过某一元素，因为是有序的，只需判断used[i-1] ，nums[i-1]===nums[i]
现在得到题目是无序的，使用set，每次循环判断当前数字是否在set中，如果在，跳过，否则将数字放入set，实现去重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
var findSubsequences = function(nums) {
  let path = []
  let res = []
  // 回溯算法函数
  const backTraking = (nums,startIndex)=>{
    // 收获结果的地方
    if (path.length > 1){
      res.push([...path])
    }
    // 终止条件
    if (startIndex >= nums.length){
      return
    }
    //单层搜索逻辑
    let set = new Set()
    for(let i=startIndex;i<nums.length;i++){
      // 当前元素小于path最后的元素，跳过. 但是如果path为空，不跳过
      if (nums[i] < path[path.length-1] || !path ){
        continue
      }
      // 树层去重
      if(set.has(nums[i])){
        continue
      }
      else{
        set.add(nums[i])
      }
      path.push(nums[i])
      backTraking(nums,i+1)
      path.pop()
    }
  }
  backTraking(nums,0)
  return res
};

全排列

https://leetcode.cn/problems/permutations/description/

首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。

可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。

但排列问题需要一个used数组，标记已经选择的元素，如图橘黄色部分所示:
图 15

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
var permute = function(nums) {
  let path =[]
  let res = []
  let used = new Array(nums.length).fill(false)
  const backTracking = (nums)=>{
    if(path.length === nums.length){
      res.push([...path])
      return
    }
    for(let i=0; i<nums.length; i++){
      if(used[i]){
        continue
      }
      used[i] = true
      path.push(nums[i])
      backTracking(nums)
      path.pop()
      used[i] = false
    }
  }
  backTracking(nums)
  return res
};

全排列II

https://leetcode.cn/problems/permutations-ii/description/

加一个数层去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var permuteUnique = function(nums) {
  let path = []
  let res = []
  // 用于排列
  let used = new Array(nums.length).fill(false)
  // 用于数层去重
  let used1 = new Array(nums.length).fill(false)
  nums.sort((a,b)=>a-b)
  const backTracking = (nums)=>{
    // 终止条件
    if(path.length === nums.length){
      res.push([...path])
      return
    }
    for(let i=0; i<nums.length; i++){
      if (used[i]){
        continue
      }
      //树层去重
      if(i>0 && nums[i] === nums[i-1] && !used1[i-1]){
        continue
      }
      used[i] = true
      used1[i] = true
      path.push(nums[i])
      backTracking(nums)
      path.pop()
      used[i] = false
      used1[i] = false
    }
  }
  backTracking(nums)
  return res
};

重新安排行程

https://leetcode.cn/problems/reconstruct-itinerary/description/

N皇后

https://leetcode.cn/problems/n-queens/

图 16

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
var solveNQueens = function(n) {
  let res = []
  // Array.from() 是一个静态方法，它从类数组或可迭代对象创建一个新的数组实例。
  let checkboard = Array.from({length:n},()=>Array.from({length:n},()=>'.'))
  const isVaild = (row,col,checkboard,n)=>{
    // 检查列,只需要检查当前行上面的行
    for(let i=0;i<row;i++){
      if(checkboard[i][col] === 'Q'){
        return false
      }
    }
    // 检查左上方45度对角线
    for(let i= row-1,j=col-1;i>=0 && j>=0;i--,j--){
      if(checkboard[i][j] === 'Q'){
        return false
      }
    }
    // 检查右上方45度对角线
    for(let i=row-1,j=col+1;i>=0 && j<n;i--,j++){
      if(checkboard[i][j] === 'Q'){
        return false
      }
    }
    return true
  }

  const backTraking = (checkboard,n,row)=>{
    if(row==n){
      res.push(checkboard.map(row=>row.join('')))
      return
    }
    for (let col=0;col<n;col++){
      //判断放在这里是否符合要求
      if (isVaild(row,col,checkboard,n)){
        checkboard[row][col] = 'Q'
        backTraking(checkboard,n,row+1)
        checkboard[row][col] = '.'
      }
    }
  }
  backTraking(checkboard,n,0)
  return res
};

解数独

https://leetcode.cn/problems/sudoku-solver/
https://www.programmercarl.com/0037.%E8%A7%A3%E6%95%B0%E7%8B%AC.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
var solveSudoku = function (board) {
  function isValid(row, col, val, board) {
    let len = board.length
    // 行不能重复
    for (let i = 0; i < len; i++) {
      if (board[row][i] === val) {
        return false
      }
    }
    // 列不能重复
    for (let i = 0; i < len; i++) {
      if (board[i][col] === val) {
        return false
      }
    }
    // 3*3的格子不能重复
    let startRow = Math.floor(row / 3) * 3 // 0,3,6
    let startCol = Math.floor(col / 3) * 3 // 0,3,6

    for (let i = startRow; i < startRow + 3; i++) {
      for (let j = startCol; j < startCol + 3; j++) {
        if (board[i][j] === val) {
          return false
        }
      }
    }
    return true
  }

  function backTracking() {
    for (let i = 0; i < board.length; i++) {
      for (let j = 0; j < board[0].length; j++) {
        if (board[i][j] !== '.') continue
        for (let val = 1; val <= 9; val++) {
          if (isValid(i, j, `${val}`, board)) {
            board[i][j] = `${val}`
            if (backTracking()) {
              return true
            }

            board[i][j] = `.`
          }
        }
        return false
      }
    }
    return true
  }
  backTracking(board)
  return board
};

LCR 121寻找目标值

发表于2024-03-29更新于2024-03-29

LCR 121寻找目标值

我的思路

我的思路，很混乱。因为有两个方向，向下向右都增大，我就不知道该向下还是向右了。然后设计了很多情况，最后发现条件都理不顺。哭了

转变成树的思路

把数组旋转45度，他就变成了树，节点的左节点比根小，右节点比根大。问题就得到了解决

图 0

解题思路如下：

  • 确定根节点，以右上角为根节点，设置索引i=0,j=plants[0].length
  • 当 plants[i][j] > target那么找左子节点，即j--
  • 当 plants[i][j] < target那么找右子节点，即i++
  • 当 plants[i][j] = target return true
  • 若行索引或列索引越界，表示没找到目标值，返回false
  • 最后补充注意点，测试时发现有的用例是空数组，所以要在函数中判断这种情况，遇到直接return false
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var findTargetIn2DPlants = function (plants, target) {
  //特殊情况判断，空数组，return false
  if (plants.length === 0) return false;

  const r = plants.length;
  const c = plants[0].length;
  // 通过i,j确定根节点为右上角
  let i = 0;
  let j = c - 1;
  // 从右上角开始查找
  while (i < r && j >= 0) {
    if (plants[i][j] === target) {
      return true;
    } else if (plants[i][j] > target) {
      j--;
    } else {
      i++;
    }
  }
  return false;
};

LCR 128.库存管理

发表于2024-03-29更新于2024-03-29

库存管理(寻找旋转排序数组最小值)

题目

图 0
图 1

解题

我的思路

我知道最小值的位置的特点是，该位置的数小于其前一个位置的数，当然这里存在一个特殊点是当这个位置为0时，没有前一个数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//没写出来
var findMin = function(nums) {
    // 特点在于，目标数的前一位大于目标数
    //特殊情况是目标数的下表为0，说明旋转了0次
    let left = 0,right = nums.length
    while(left<right){
        let mid = left + Math.floor((right - left)/2)
        if(mid === 0) return nums[mid]
        else{
            if(nums[mid] < nums [mid-1]) return nums[mid]
            else if()
        }

    }
};

正确思路

我们可以认为这个数组是由重复值的。那么一个经过旋转之后的数组可视化后如下图所示。数组中最后一个元素的大小为x，如图中虚线所示。

它具如下的特点：

  • 最小值右边的元素均小于等于x
  • 最小值左边的元素均大于等于最小值

    基于上述特性才使得本题可以使用二分查找法解决。

图 3

二分查找的情况可以分为3类
在二分查找的每一步中，左边界为 low，右边界为 high，区间的中点为 pivot，最小值就在该区间内。我们将中轴元素 nums[pivot]与右边界元素 nums[high]进行比较，可能会有以下的三种情况：

1、nums[pivot] > nums[high],说明最小值在pivot与high之间。low = pivot + 1

图 4

2、nums[pivot] < nums[high],说明最小值不在在pivot与high之间。high = pivot - 1

图 5

3、nums[pivot] === nums[high],这是由于存在重复值。high=high-1

图 6

当二分查找结束时，我们就得到了最小值所在的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var stockManagement = function(stock) {
  let low = 0;
    let high = stock.length - 1;
    while (low < high) {
        const pivot = low + Math.floor((high - low) / 2);
        if (stock[pivot] < stock[high]) {
            high = pivot;
        } else if (stock[pivot] > stock[high]) {
            low = pivot + 1;
        } else {
            high -= 1;
        }
    }
    return stock[low];
};

LCR 127.跳跃训练

发表于2024-03-29更新于2024-03-29

跳跃训练

题目

图 0

我的求解

这道题我很有印象，和爬楼梯是同一个意思。就是要用到动态规划。逻辑在于我要到达第n个格子的方法，等于我要到达第n-1个格子的方法加到达n-2个格子的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var trainWays = function(num) {
  //和爬楼梯很像，是动态规划的题目
  //dp[i]表示跳到第i个台阶的方法数
  let dp = new Array(num + 1).fill(0)
  dp[0] = 1
  dp[1] = 2
  //这里有一些特殊情况，第一种是在程序提交不同过的例子中发现的，
  if (num === 0) return dp[0]
  //第二种就是只有一个格子
  if (num === 1) return dp[0]
  //第三种只有两个格子的情况。
  if (num === 2) return dp[1]
  else {
    for (let i = 2; i < num; i++) {
      //别忘了题目要求的取模
      dp[i] = (dp[i - 1] + dp[i - 2]) % 1000000007
    }
    return dp[num - 1]
  }
};

合并两个有序数组

发表于2024-03-28更新于2024-04-26

合并两个有序数组

题目

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

求解

https://leetcode.cn/problems/median-of-two-sorted-arrays/solutions/258842/xun-zhao-liang-ge-you-xu-shu-zu-de-zhong-wei-s-114/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function(nums1, nums2) {
  // 保证nums1的较短数组
  if (nums1.length > nums2.length) {
    [nums1, nums2] = [nums2, nums1];
  }
  //m为较短数组的长度,n为较长数组的长度
  let m = nums1.length; // Add missing variable declaration for m
  let n = nums2.length; // Add missing variable declaration for n
  // 左边元素的个数
  let totalLeft = Math.floor((m + n + 1) / 2);
  // 在nums1的[0,m]中找合适的分割线
  // 使得nums1[i-1] <= nums2[j] && nums2[j-1] <= nums1[i]
  let left = 0, right = m;
  // 二分查找
  while(left < right){ // Fix the loop condition
    let i = left + Math.floor((right - left + 1) / 2);
    let j = totalLeft - i;
    if(nums1[i-1] > nums2[j]){
      //下一轮搜索区间在[left,i-1]
      right = i-1;
    }
    else{
      //下一轮搜索区间在[i,right],注意当这个区间只有两个元素时，会陷入死循环，因此在二分的时候要+1
      left = i
    }
  }
  //退出循环后找到了想要的分割线
  let i = left;
  let j = totalLeft - i;
  // 定义左右两边的四个值,还是为了适应特殊情况
  // 如果 i 等于 0，说明 nums1 的左侧没有元素，所以左侧最大值设为负无穷 -Infinity。否则，左侧最大值就是 nums1[i-1]。
  //左侧找最大值，右侧找最小值
  let nums1LeftMax = i === 0 ? -Infinity : nums1[i-1];
  let nums1RightMin = i === m ? Infinity : nums1[i];
  let nums2LeftMax = j === 0 ? -Infinity : nums2[j-1];
  let nums2RightMin = j === n ? Infinity : nums2[j];
  // 如果总长度是奇数
  if((m + n) % 2 === 1){
    return Math.max(nums1LeftMax, nums2LeftMax);
  }
  else{
    return (Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin)) / 2;
  }
};

二分查找

一看就会，一写就废。问题出在边界无法掌握，一不小心就死循环了，因此要掌握二分查找的边界
https://blog.csdn.net/qq_45978890/article/details/116094046

二分查找的条件

  • 有序
  • 只找一个

二分查找的边界

  • 1、[左闭，右闭]

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    const search1 = (arr, target) => {
      let left = 0, right = arr.length - 1;
      // 二分查找,闭区间
      while (left <= right) {  // 因为是闭区间，所以left 要小于等于right
        let mid = left + Math.floor((right - left) / 2);
        if (arr[mid] < target) { // 目标值在右边
          left = mid + 1;  //应为是左闭右闭，所以不用担心，边界mid+1后mid+1不能被比较
        }
        else if (arr[mid] > target) { // 目标值在左边
          right = mid - 1;
        } else {
          // 找到目标值
          return mid;
        }
      }
      return -1;
    }
    //犯个错误，第二个else if，我用了if，然后下面用了else，导致第二个if和最后的else成了组合，不再能表示所有情况。
    console.log(search([1,2,3,4,5,6,7,8,9], 5)) // 4

  • 2、[左闭，右开)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    const search = (arr, target) => {
      let left = 0, right = arr.length; // 左闭右开区间
      while (left < right) { //终止条件
        let mid = left + Math.floor((right - left) / 2);
        if (arr[mid] < target) { // 目标值在右边
          left = mid + 1; // 更新左边界
        } else if (arr[mid] > target) {  // 目标值在左边
          right = mid; // 更新右边界
        } else {
          return mid;
        }
      }
    }

  • 3、(左开，右闭]

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    //左开右闭区间
    const search = (arr, target) => {
      let left = -1, right = arr.length - 1; // 左开右闭区间
      while (left < right) { //终止条件
        let mid = left + Math.floor((right - left + 1) / 2);
        if (arr[mid] < target) { // 目标值在右边
          left = mid; // 更新左边界
        } else if (arr[mid] > target) {  // 目标值在左边
          right = mid - 1; // 更新右边界
        } else {
          return mid;
        }
      }
    }

  • 4、开区间写法

const search4 = (arr, target) => {
  let left = -1, right = arr.length; // 开区间
  while (left + 1 < right) { //终止条件
    let mid = left + Math.floor((right - left) / 2);
    if (arr[mid] < target) { // 目标值在右边
      left = mid; // 更新左边界
    } else if (arr[mid] > target) {  // 目标值在左边
      right = mid; // 更新右边界
    } else {
      return mid;
    }
  }
}```

ref和reactive的区别

发表于2024-03-20更新于2024-03-20

ref和reactive的区别

1、ref适合监听基本数据类型，reactive监听复杂数据类型，如果让reactive监听基本数据类型，需要将其写对象模式，浪费空间。
2、reactive通过Proxy返回一个代理对象实现响应,ref通过defineProperty实现。

vue2中ref和vue3中ref的区别

在vue2中，ref主要是用来标识结点和组件的，相当于dom里面的id
在vue3中，vue团队重写了ref,主要通过ref来创建响应式元素，并且继承了vue2中的标识作用

在Vue 2中，ref的主要作用是在模板中获取DOM元素或组件实例。在Vue 3中，除了可以获取DOM元素或组件实例，还可以将一个基本类型的变量转换成响应式的数据，并且不用再通过复杂的步骤来访问响应式数据。Vue 3的ref还支持对象属性和数组索引来访问组件属性或DOM元素。

在Vue 2中，ref是一个帮助我们在模板中访问DOM元素或组件实例的API。例如，我们可以使用ref来访问一个表单输入框的值或组件实例的方法。在Vue 2中，ref还可以用于在父子组件之间进行通信，通过在父组件中使用ref为子组件创建引用来访问子组件实例。

在Vue 3中，ref的用途和Vue 2中一样，但它还有一些重要的新功能。在Vue 3中，ref可以包含更多类型的值，例如普通的Javascript变量、响应式的数据和一个函数。此外，Vue 3中的ref还可以用作类似于reactive函数的入口，将一个基本数据类型转换为响应式数据。而且Vue 3中的ref在访问响应式数据时，会自动进行解包和提取值，免去了Vue 2中通过$refs访问的繁琐步骤。最后，Vue 3中的ref还可以通过对象属性和数组索引来访问组件的属性或组件内的DOM元素。

原文链接：https://blog.csdn.net/qq_68805187/article/details/130856718

defineProperty和proxy的区别

发表于2024-03-20更新于2024-03-20

defineProperty和proxy的区别

响应式的目的

当对象属性被读取后，被修改后，我要介入进行一些操作。
属性值的读和修改变成函数

defineProperty

他是针对属性的监听，所以对obj下的每个属性(深度遍历)进行监听。
天生缺陷：深度遍历效率缺失；由于遍历，新增属性他是没有被监听的；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const obj = {
  a:1,
  b:2,
  c:{
    d:3,
    e:4
  },
}
function _isObject(v){
  return typeof v==='object' && v != null
}
function observe(obj){
  for(const k in obj){
    let v = obj[k]
    if (_isObject(v)){
      observe(v)
    }
    Object.defineproperty(obj,'a',{
    get(){
      console.log('a','读取')
      return v
    },
    set(newval){
      if(v != newval){
        v = newval
        console.log('a','更改')
      }
    }
  })
  }
}

proxy监听整个对象

Proxy返回一个新的代理对象，不动原数据
监听的是整个对象，所以不需要遍历，新增时可以收到通知

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
const obj = {
  a:1,
  b:2,
  c:{
    d:3,
    e:4
  },
}
function _isObject(v){
  return typeof v==='object' && v != null
}

function observe(obj){
  const proxy = new Proxy(obj,{
    get(target,k){
      let v = target[k]
      if(_isObject(v)){ //这里是有递归，但只有v被读到才会触发。
        observe(v)
      }
      console.log(k,'读取')
      return v
    },
    set(target,k,val){
      if(target[k] != val){
        target[k] = val
      }
    }
  })
  return proxy
}

const proxy = new Proxy(obj,{
  get(target,k){
    let v = target[k]
    console.log(k,'读取')
    return v
  },
  set(target,k,val){
    if(target[k] != val){
      target[k] = val
    }
  }
})

26.删除有序数组中的重复项

发表于2024-03-14更新于2024-03-29

删除有序数组中的重复项

题目：https://leetcode.cn/problems/remove-duplicates-from-sorted-array/description/

图 0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 方法一：遍历数组，splice删除重复项
var removeDuplicates = function(nums) {
  for(let i = 0; i<nums.length; i++){
    let j = i+1
    while(nums[i] == nums[j]){
      nums.splice(i, 1)    //我一直再写j++，其实没必要，因为数据已经被删除了
    }
  }
};

//方法二：双指针
var removeDuplicates = function(nums) {
  let p=0,q=1   //前后指针
  while(q<nums.length){
    if(nums[p] != nums[q]){
      nums[p+1] = nums[q]
      p++
    }
   q++
  }
  return p+1
};

Mock的使用

发表于2024-03-14更新于2024-03-29

Mock的使用

Mock是什么

Mock（模拟）是一种常用的测试手段。Mocking 是在测试过程中，对于某些不容易构造或者不容易获取的对象，用一个虚假的对象来创建以便测试的方法。

你可能有一个函数，它需要从数据库中获取数据。在测试这个函数时，你可能不想真的去连接数据库，因为这会使测试变得复杂并且慢。这时，你可以创建一个 Mock 对象来模拟数据库的行为。你可以预设这个 Mock 对象的行为，让它返回你想要的数据，然后在测试中使用这个 Mock 对象，而不是真正的数据库。

Mockjs官网 https://github.com/nuysoft/Mock/wiki/Getting-Started

Mock安装与配置

安装
1
pnpm install -D vite-plugin-mock mockjs
配置vite.config.js文件
1
2
3
4
5
6
7
8
9
10
11
12
13
import { UserConfigExport, ConfigEnv } from 'vite'
import { viteMockServe } from 'vite-plugin-mock'
import vue from '@vitejs/plugin-vue'
export default ({ command })=> {
  return {
    plugins: [
      vue(),
      viteMockServe({  //保证开发期间可以使用访问mock提供的数据
        localEnabled: command === 'serve',
      }),
    ],
  }
}

在整个项目的根路径新建一个mock文件夹，在此文件夹中新建一个用户文件user.ts

Mock模拟数据和接口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
//用户信息数据
//createUserList函数执行会返回一个数组，数组里面包含两个用户信息
function createUserList() {
    return [
        {
            userId: 1,
            avatar:
                'https://wpimg.wallstcn.com/f778738c-e4f8-4870-b634-56703b4acafe.gif',
            username: 'admin',
            password: '111111',
            desc: '平台管理员',
            roles: ['平台管理员'],
            buttons: ['cuser.detail'],
            routes: ['home'],
            token: 'Admin Token',
        },
        {
            userId: 2,
            avatar:
                'https://wpimg.wallstcn.com/f778738c-e4f8-4870-b634-56703b4acafe.gif',
            username: 'system',
            password: '111111',
            desc: '系统管理员',
            roles: ['系统管理员'],
            buttons: ['cuser.detail', 'cuser.user'],
            routes: ['home'],
            token: 'System Token',
        },
    ]
}

export default [
    // 用户登录接口
    {
        url: '/api/user/login',//请求地址
        method: 'post',//请求方式
        response: ({ body }) => {
            //获取请求体携带过来的用户名与密码
            const { username, password } = body;
            //调用获取用户信息函数,用于判断是否有此用户
            const checkUser = createUserList().find(
                (item) => item.username === username && item.password === password,
            )
            //没有用户返回失败信息
            if (!checkUser) {
                return { code: 201, data: { message: '账号或者密码不正确' } }
            }
            //如果有返回成功信息
            const { token } = checkUser
            return { code: 200, data: { token } }
        },
    },
    //对外暴露一个数组，
    //数组中包含登录假接口
    //还有一个获取用户信息得到假的接口
    {
        url: '/api/user/info',
        method: 'get',
        response: (request) => {
            //获取请求头携带token
            const token = request.headers.token;
            //查看用户信息是否包含有次token用户
            const checkUser = createUserList().find((item) => item.token === token)
            //没有返回失败的信息
            if (!checkUser) {
                return { code: 201, data: { message: '获取用户信息失败' } }
            }
            //如果有返回成功信息
            return { code: 200, data: {checkUser} }
        },
    },
]

vue 的响应式框架 （1.0）

发表于2024-03-14更新于2024-03-15

vue 的响应式框架 （1.0）

思路：属性发生变化时，调用依赖这些属性的函数

一、实现的过程需要解决以下一些问题

  • 1.如何追踪属性发生了变化
  • 2.如何知道该属性被哪些依赖使用
  • 3.如何执行依赖的函数
  • 4.如何避免重复执行依赖的函数

二、基础知识

object.defineProperty(obj, prop, descriptor)方法介绍

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//定义一个对象
var obj = {
  name: '张三',
  age : 20
}

object.defineProperty(obj,name){
  get:function(){
    console.log('有人读取了name属性')
    return obj.name
  }
  set function(val){  //obj中的name发生那个变化后，会调用set函数。因此可在这里调用其依赖函数
    obj.name = val
    console.log('有个家伙在给name属性赋值')
  }
}

去重

1
2
3
4
5
6
7
//方法一：Set集合，可以判断，如果当前的值和之前的值相同，则不执行依赖函数
let funcs = new Set()
//方法二：ES6中的includes方法，判断当前的值是否在数组中，如果在，则不执行依赖函数
let funcs = []
if (!funcs.includes(func)) {
  funcs.push(func)
}

三、难点

此时我们已经解决了问题1和问题4，也知道了依赖函数应该在set中执行。那么如何知道属性被哪些依赖使用呢？

1
2
3
4
5
// 不直接运行函数，而是使用定义一个全局变量，这样只要使用这个统一变量的名称运行函数，就能拿到函数了
window.__func = func1
  func1()
window.__func = null
//这样只需在get中添加window.__func到数组即可

四、实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//首先新建一个js，在这个新的js中实现上述代码
//定义一个观察者，监视对象的属性
function Observer(obj) {
  for (const key in obj){
    let intervalValue = obj[key]
    let observers = new Set()    //用来保存相关依赖
    //使用Object.defineProperty()方法，给obj的key属性添加get和set方法
    defineProperty(obj, key, obj[key]){
      get: function(){
        if (window.__func){  //存在说明有函数在运行，是哪个函数呢，那个函数名使用window.__func可以访问到
          observers.add(window.__func)
        }
        return intervalValue
      },
      set: function(val){
        console.log('有人修改了' + key + '属性，我要去通知我的订阅者了')
        obj[key] = val
        //通知所有的订阅者,重新运行
        observers.forEach(observer => observer())
      }
    }
  }
}

// 定义一个统一执行函数的函数
function autoRun(fn){
window.__func = fn
fn()
window.__func = null
  }

//函数调用时用autoRun不要直接运行
autoRun(func1())
autoRun(func2())